Modules Ecologia Numérica Descrição de comunidades biológicas
Descrição de comunidades biológicas

Os atributos de uma communidade biológica são simples, em princípio
- Entidades
- Identidades
- Quantidades
Exercício Comunidades Culinárias (para etregar na forma de um Rpubs até 30 de dezembro de 2022)
Fizemos um exercício muito bom em sala de aula. Criamos uma comunidades biológica com grãos e massa para simular a montagem de uma comundaidade biológica em uma ilha oceânica recém formada. Dois grupos fizeram amostragem: um grupo usou uma técnica de alatorização das amostras, soirtendo quadrados que correspondiam a 10% da área da ilha. O outro grupo usou outra tepcnica: usou dois transectos localizados de maneira planejada para maximizar a captura da diverisdade da ilha. A base de dados que geramos pode ser obtida NESTE LINK.
Agora, você precisa repetir os passos abaixo, mas fazer um esforço para comentar cada passo de exercício
Passo 1) Subir os dados no R
base<-read.csv("https://raw.githubusercontent.com/fplmelo/ecoaplic/main/content/collection/eco_num/com_cul.csv", row.names = 1) # atenção, use o caminho onde você guardou a base que baixou anteriormente
base # mostra a base. confira se está tudo ok
## q1 q2 q3 q4 q5 q6 q7 q8 q9 q10 t1 t2 t3 t4 t5 t6 t7 t8 t9 t10
## arroz_c 0 1 7 6 1 4 4 1 1 5 3 8 5 6 3 0 0 0 0 3
## arroz_e 1 0 0 1 0 0 8 4 0 3 0 1 8 1 1 0 0 0 1 0
## milho 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## ervilha 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0
## feijao_preto 0 0 0 0 0 0 0 0 0 0 0 0 6 0 0 0 0 0 0 0
## carioca_c 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 1
## carioca_e 0 0 0 2 2 0 0 0 0 8 0 0 0 0 0 0 0 0 0 0
## mac_paraf 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
## mac_tubo 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## mac_espag 0 0 0 3 1 0 0 0 6 4 16 9 0 0 0 0 2 2 1 0
passo 2) Começar a explorar a base
Vamos separar as bases, e ver suas dimensões e checar se tudo está correto.
Atenção: use os comandos ‘dim()’, ‘nrow()’, ‘ncol()’, ‘rowSums()’ e ‘colSums()’ para cada base e vá montando seu arquivo com os resutlados comentados.
ver exemplo abaixo.
# Notem que usei "echo=FALSE" para não aparecer os resultados e não ficar muito longo, mas deixem o seu como TRUE
base_q<-base[,1:10] # criamos a base dos quadrados
base_t<-base[,11:20] # criamos também a base dos transectos
# chequem as bases com o comando abaixo
base_q
## q1 q2 q3 q4 q5 q6 q7 q8 q9 q10
## arroz_c 0 1 7 6 1 4 4 1 1 5
## arroz_e 1 0 0 1 0 0 8 4 0 3
## milho 0 0 0 0 0 0 0 0 0 0
## ervilha 0 0 1 0 0 0 1 0 0 0
## feijao_preto 0 0 0 0 0 0 0 0 0 0
## carioca_c 0 0 1 1 0 0 0 0 0 0
## carioca_e 0 0 0 2 2 0 0 0 0 8
## mac_paraf 0 0 0 0 0 0 0 0 0 0
## mac_tubo 0 0 0 0 0 0 0 0 0 0
## mac_espag 0 0 0 3 1 0 0 0 6 4
base_t
## t1 t2 t3 t4 t5 t6 t7 t8 t9 t10
## arroz_c 3 8 5 6 3 0 0 0 0 3
## arroz_e 0 1 8 1 1 0 0 0 1 0
## milho 0 0 0 0 0 0 0 0 0 0
## ervilha 0 0 1 0 0 0 0 0 0 0
## feijao_preto 0 0 6 0 0 0 0 0 0 0
## carioca_c 0 0 0 0 0 2 0 0 0 1
## carioca_e 0 0 0 0 0 0 0 0 0 0
## mac_paraf 0 0 0 0 0 0 1 0 0 0
## mac_tubo 0 0 0 0 0 0 0 0 0 0
## mac_espag 16 9 0 0 0 0 2 2 1 0
dim(base_q) # Tabela formada por 10 linhas e 10 colunas
## [1] 10 10
colSums(base_t) # abundâncias de cada amostra da base de transectos
## t1 t2 t3 t4 t5 t6 t7 t8 t9 t10
## 19 18 20 7 4 2 3 2 2 4
## Explore...
passo 3) Fazendo perguntas
Qual o número de espécies dos diferentes métodos?
library(vegan)# Esse pacote tem um monte de análises massa para ecólogos
library(tidyverse)
specnumber(t(base_q)) # espécies de cada amostra... mas como saber o número total de espécies?
## q1 q2 q3 q4 q5 q6 q7 q8 q9 q10
## 1 1 3 5 3 1 3 2 2 4
base_q %>% # Aq2ui eu criei minha solição...
rownames_to_column("species") %>% # trouxe de volta o nomes das linhas para uma coluna
mutate(ab_spe=rowSums(base_q)) %>% # Criei uma coluna nova com as somas das abundâncias
filter(ab_spe > 0) %>% # filtrei para reter somente as somas maiores que zero, pois os zeros são espécies ausentes
count() # contei, BINGO!
## n
## 1 6
# Há muoitas outras formas...
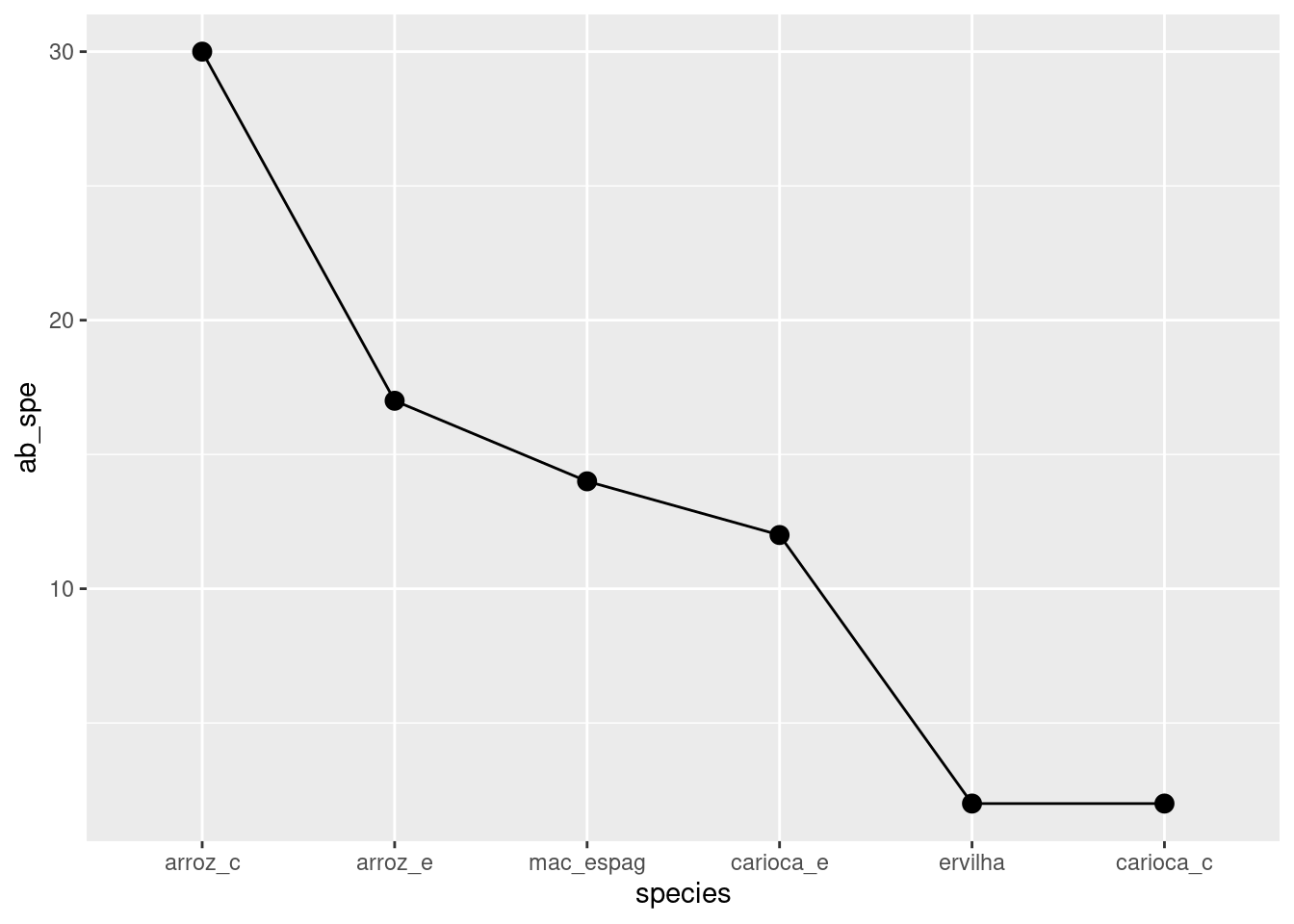
Qual a distribuição das abundâncias das espécies?
base_q %>%
rownames_to_column("species") %>%
mutate(ab_spe=rowSums(base_q)) %>%
filter(ab_spe > 0) %>% #Até aqui usei o mesmo código de antes
arrange(desc(ab_spe)) %>% #em ordem decrescente mas não fixa quando for pro ggplot, aí temos que dar outro comando
mutate(species=factor(species, level = species)) %>% #agora ele fixou as ordens
ggplot(aes(x=species, y=ab_spe))+
geom_line(group = 1)+geom_point(size = 3)->graf_abund_q
graf_abund_q
base_t %>%
rownames_to_column("species") %>%
mutate(ab_spe=rowSums(base_t)) %>%
filter(ab_spe > 0) %>% #Até atui usei o mesmo código de antes
arrange(desc(ab_spe)) %>% #em ordem decrescente mas não fixa tuando for pro ggplot, aí temos tue dar outro comando
mutate(species=factor(species, level = species)) %>% #agora ele fixou as ordens
ggplot(aes(x=species, y=ab_spe))+
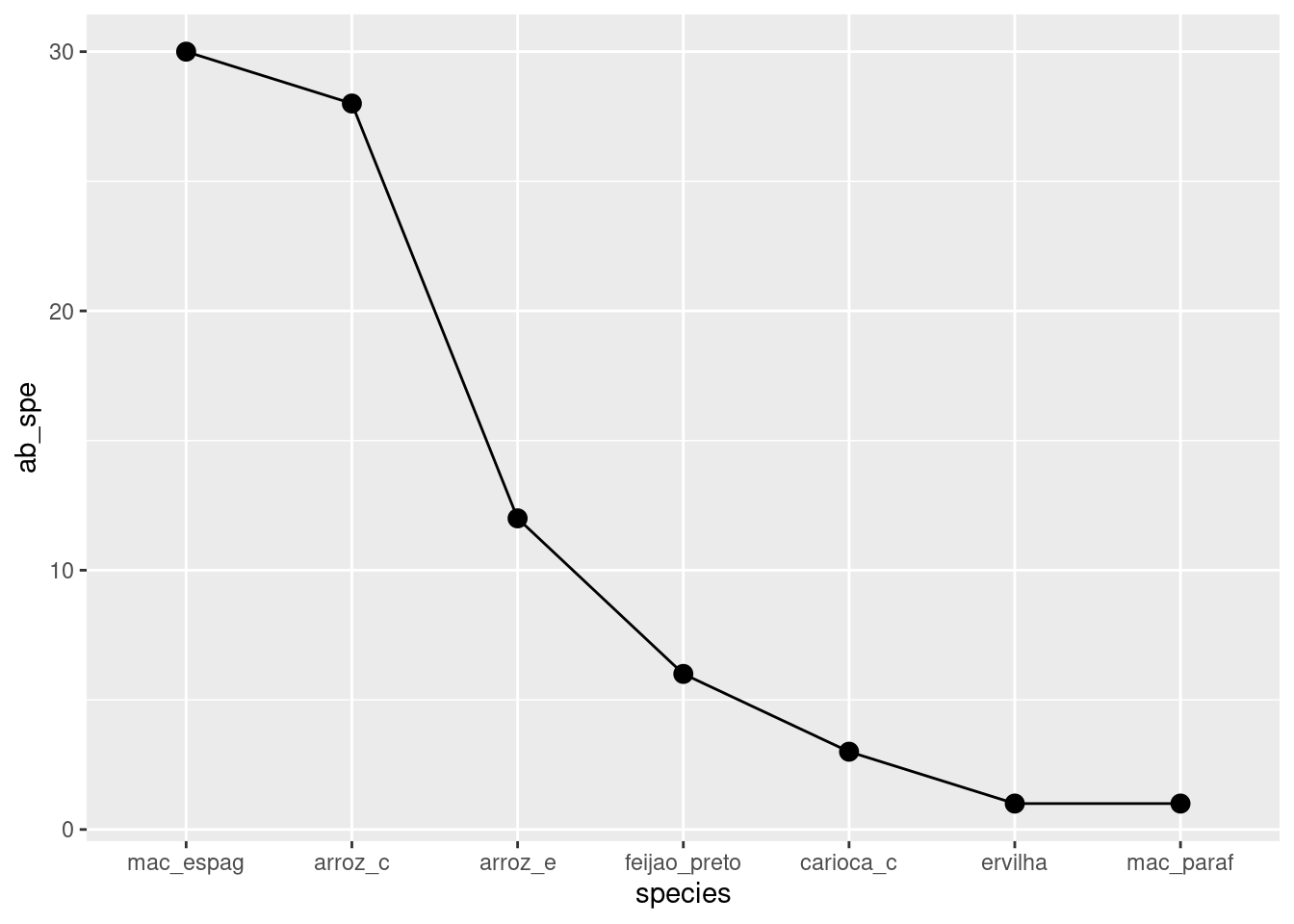
geom_line(group = 1)+geom_point(size = 3)->graf_abund_t
graf_abund_t
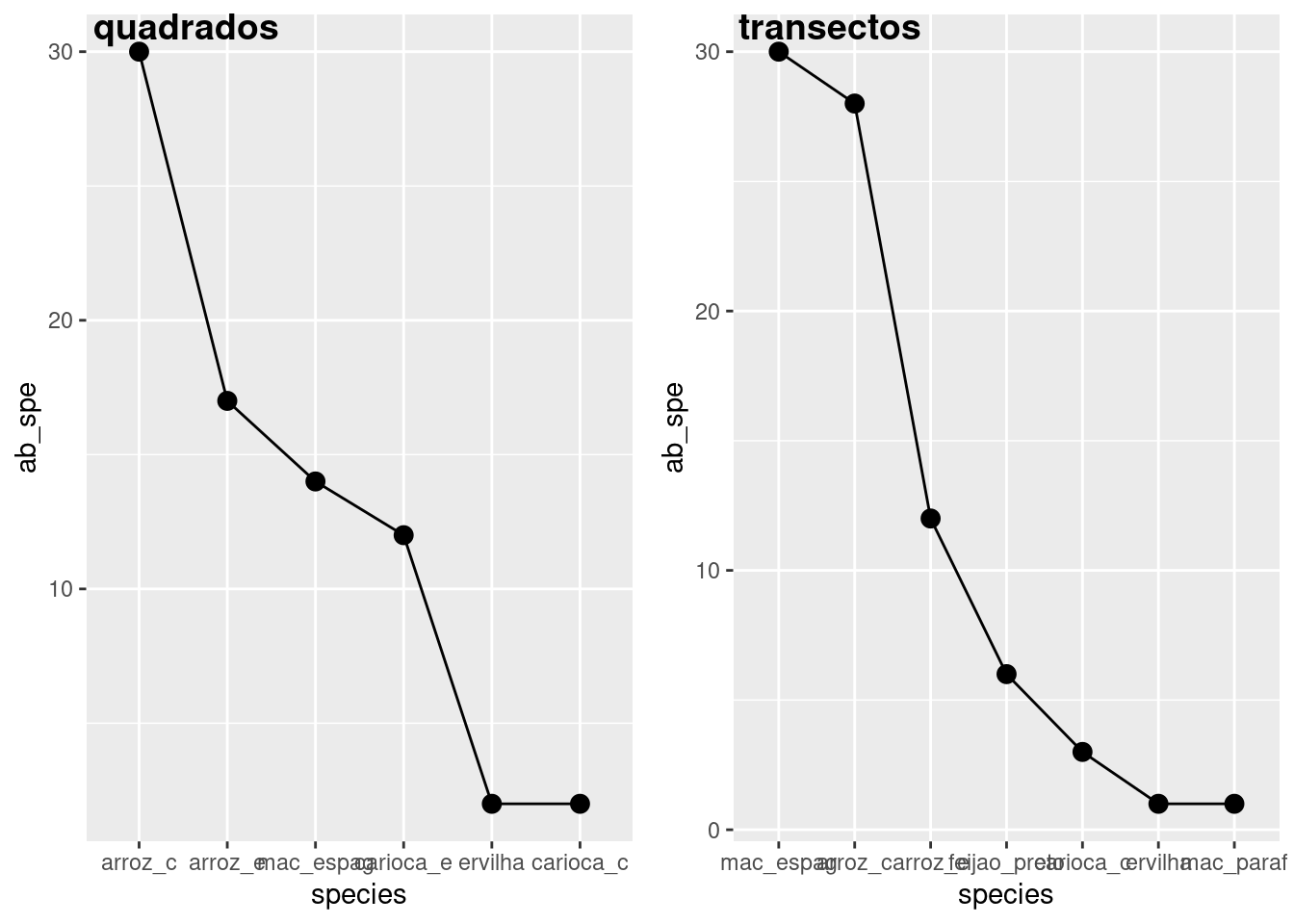
# Agora posso unir os gráficos para melhorar a vizualização
library(cowplot)
plot_grid(graf_abund_q, graf_abund_t, labels = c("quadrados", "transectos"), ncol = 2)
Estimadores de Riqueza
Note que sabemos que nenhum dos métodos capturou todas as espećies que sabíamos que existia na nossa comunidade culinária. Na natureza, porém, nunca sabemos quantas especies de fato existem. Para contornar esse problema e saber se nossas amostras são representativas, existem algumas estratpegias
Curva de rarefação
Leiam o excelente livro de Análises Ecológicas no R onde tem um capítulo sobre rarefação
Mas, aqui vamos usar nossos dados e com códigos mais simples
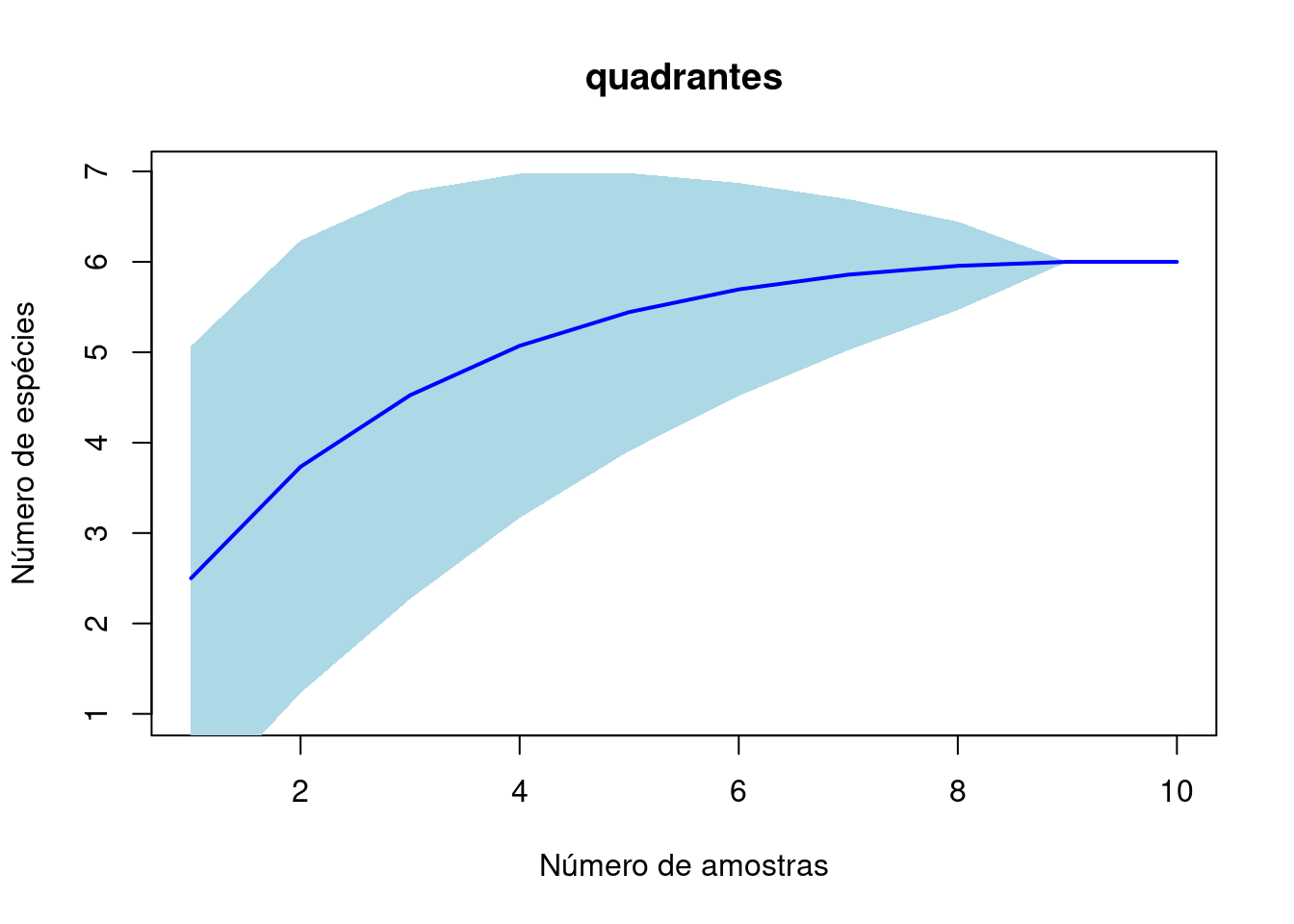
Pergunta: Será que as amostras atingiram o número real de espécies
acum_q<-specaccum(t(base_q)) # existe uma função na library vegan que faz isso... ele cria as curvas para vizualizrmos
acum_t<-specaccum(t(base_t))
plot(acum_q, ci.type = "poly", col = "blue", lwd = 2, ci.lty = 0,
ci.col = "lightblue", main = "quadrantes", xlab = "Número de amostras",
ylab = "Número de espécies")
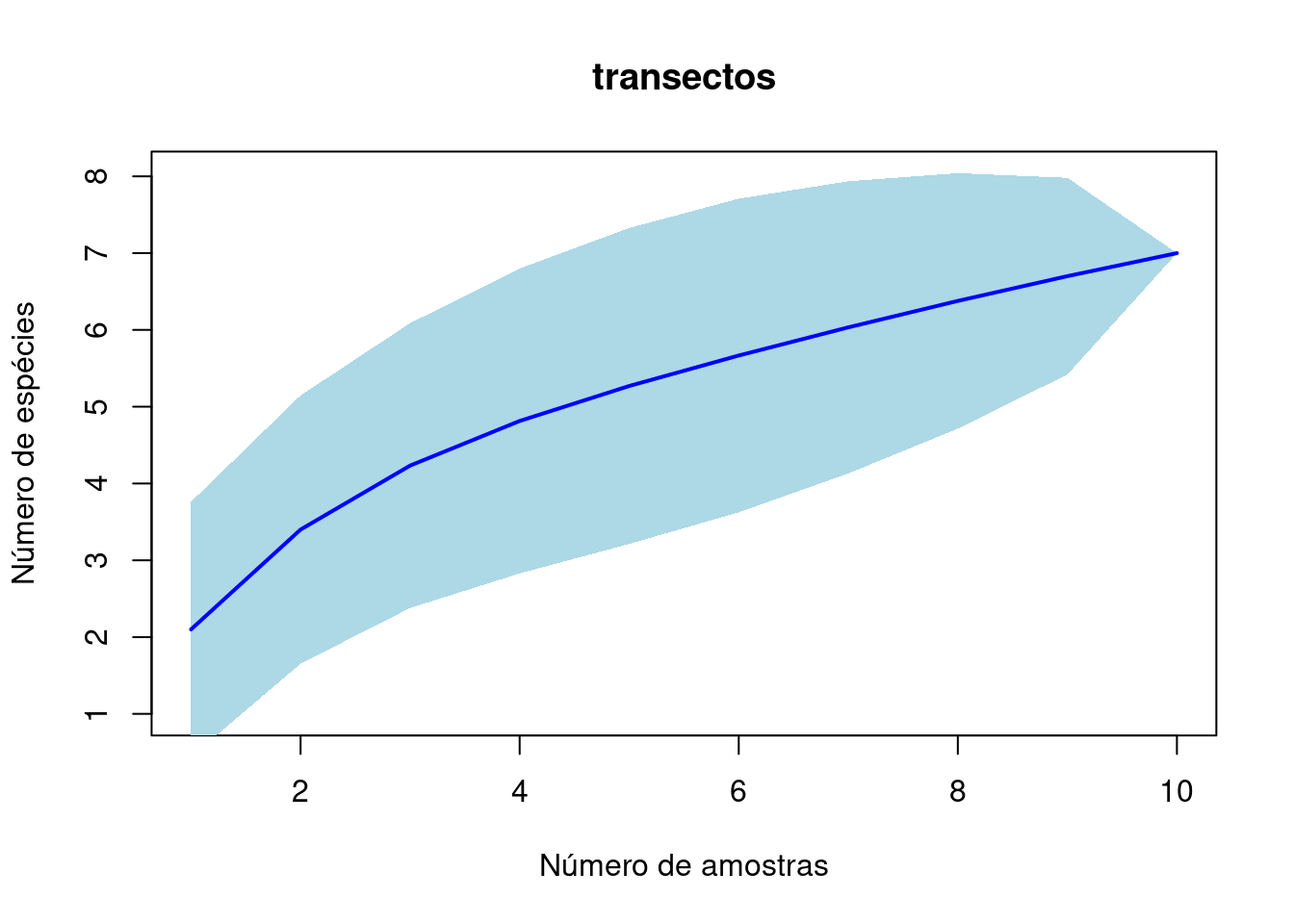
plot(acum_t, ci.type = "poly", col = "blue", lwd = 2, ci.lty = 0,
ci.col = "lightblue", main = "transectos", xlab = "Número de amostras",
ylab = "Número de espécies") # note que essa curva não parece assintotizada
specpool(base_q)# Esses são métodos de estimação de riqueza (chao, jack1, jack2, boot, etc... os .se são os valores do erro padrão)
## Species chao chao.se jack1 jack1.se jack2 boot boot.se n
## All 10 12.025 3.089144 12.7 2.056696 13.67778 11.35255 1.588261 10
specpool(base_t)# etimadores para transecto
## Species chao chao.se jack1 jack1.se jack2 boot boot.se n
## All 10 10.3 0.7035624 11.8 1.272792 9.133333 11.3759 1.480355 10
Quais estimadores forma mais fidedignos? Qual métodos obteve menos erro?
para entender e ver códigos dessa análise veja esse site
Para finalizar esse exercício, repita o que foi feito, comente seus resultados e códigos e tente clacular os índices de diversidade de Shannon e Simpson para cada um dos métodos (base_q e base_t). Comente.
Para brincar durante as férias é esse exercício abaixo (para entregar dia 30 de janeiro de 2023)
Essa é uma base de dados reais de árvores do Panamá onde muitos biólogos estudam ecologia tropical.
Vamos examinar essa comunidade
library (vegan)
library(BiodiversityR)
data (BCI)
BCI.env <- read.delim ('https://raw.githubusercontent.com/zdealveindy/anadat-r/master/data/bci.env.txt', row.names = 1)
BCI.soil <- read.delim ('https://raw.githubusercontent.com/zdealveindy/anadat-r/master/data/bci.soil.txt')
Estação Biológica de Barro Colorado

Para uma descrição completa do local de estudo clique aqui


- São dados de uma série de plots 50 permanentes e contíguos de 1ha (50 ha no total) onde todas as árvores maiores que 10cm DAP (diametro à altura do peito) e uma grande quantidade de variáveis ambientais têm sido monitoradas há décadas.
Vamos ver a estrutura dessa base dados
dim(BCI) # São 50 linhas (plots de 1 ha) e 225 colunas (espécies de árvores)
## [1] 50 225
A primeira tarefa de um ecólogo é namorar os dados. Saber coisas básicas como:
- Quantas espécies em cada amostra?
specnumber(BCI) # Sim, existe uma função para isso no pacote "vegan"
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
## 93 84 90 94 101 85 82 88 90 94 87 84 93 98 93 93 93 89 109 100
## 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
## 99 91 99 95 105 91 99 85 86 97 77 88 86 92 83 92 88 82 84 80
## 41 42 43 44 45 46 47 48 49 50
## 102 87 86 81 81 86 102 91 91 93
- Quantos indivíduos em cada amostra?
rowSums(BCI)
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
## 448 435 463 508 505 412 416 431 409 483 401 366 409 438 462 437 381 347 433 429
## 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
## 408 418 340 392 442 407 417 387 364 475 421 459 436 447 601 430 435 447 424 489
## 41 42 43 44 45 46 47 48 49 50
## 402 414 407 409 444 430 425 415 427 432
- Qual a abundância de cada espécie?
head(colSums(BCI)) # mostra somente algumas linhas, mas se remover o head(), mostra a tabela inteira
## Abarema.macradenia Vachellia.melanoceras Acalypha.diversifolia
## 1 3 2
## Acalypha.macrostachya Adelia.triloba Aegiphila.panamensis
## 1 92 23
Há funções específicas no pacote “vegan” que são muito úteis para nálises de comunidades biológica.
1 - Curvas de acumulação de espécies
Código
sp1<-specaccum(BCI, "random")
sp1
## Species Accumulation Curve
## Accumulation method: random, with 100 permutations
## Call: specaccum(comm = BCI, method = "random")
##
##
## Sites 1.00000 2.00000 3.00000 4.00000 5.00000 6.00000 7.00000
## Richness 92.17000 122.04000 138.88000 150.53000 158.52000 165.23000 170.49000
## sd 6.24428 7.14202 6.96351 6.65674 6.12245 5.94903 5.29245
##
## Sites 8.00000 9.0000 10.00000 11.00000 12.00000 13.00000 14.00000
## Richness 175.02000 178.8500 182.39000 185.04000 187.63000 190.09000 191.96000
## sd 4.86584 4.6021 4.37369 4.24721 4.15764 4.11721 4.22575
##
## Sites 15.00000 16.00000 17.00000 18.00000 19.00000 20.00000 21.00000
## Richness 193.78000 195.67000 197.31000 198.85000 200.27000 201.68000 203.00000
## sd 3.90695 4.07023 4.01938 4.13747 4.06477 3.86614 3.83235
##
## Sites 22.00000 23.00000 24.00000 25.00000 26.00000 27.00000 28.00000
## Richness 204.27000 205.54000 206.56000 207.88000 208.82000 209.86000 210.82000
## sd 3.84249 3.75895 3.62739 3.42091 3.34356 3.39346 3.24233
##
## Sites 29.00000 30.00000 31.00000 32.00000 33.00000 34.00000 35.00000
## Richness 211.90000 212.80000 213.70000 214.47000 215.25000 216.06000 216.77000
## sd 3.38893 3.34845 3.17025 2.93173 2.80106 2.69613 2.68123
##
## Sites 36.00000 37.00000 38.00000 39.000 40.00000 41.00000 42.00000
## Richness 217.53000 218.29000 218.93000 219.640 220.14000 220.72000 221.28000
## sd 2.53642 2.41333 2.32359 2.158 2.11784 2.09415 1.80951
##
## Sites 43.00000 44.00000 45.00000 46.00000 47.00000 48.00000 49.00000
## Richness 221.79000 222.22000 222.85000 223.38000 223.86000 224.25000 224.69000
## sd 1.81628 1.71494 1.57874 1.31641 1.09194 0.96792 0.63078
##
## Sites 50
## Richness 225
## sd 0
Plot
plot(sp1, ci.type="poly", col="blue", lwd=2, ci.lty=0, ci.col="lightblue")
boxplot(sp1, col="yellow", add=TRUE, pch="+")
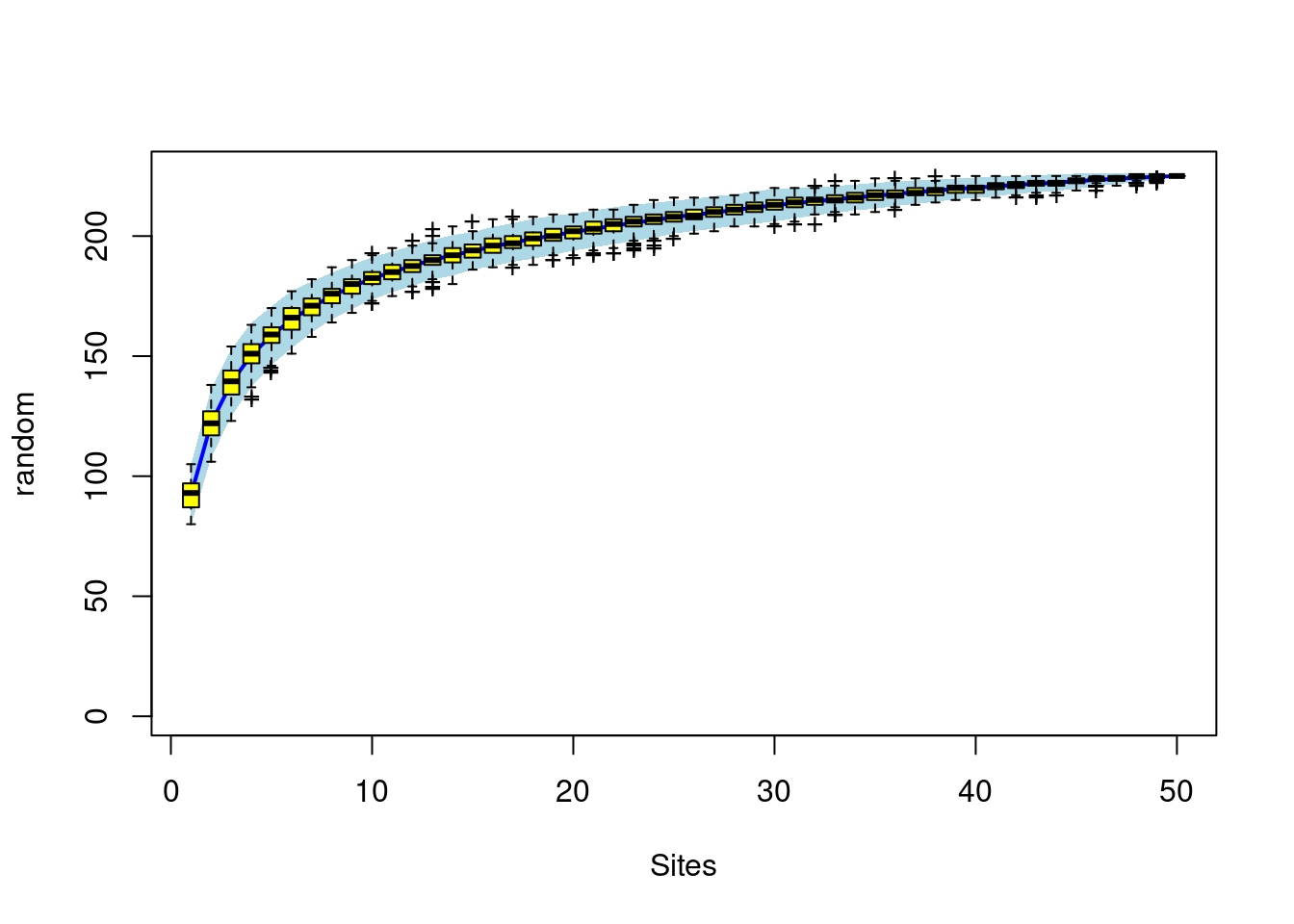
2 - Curvas de rank-abunbdância
Código
mod <- rad.lognormal(BCI[5,])
mod
##
## RAD model: Log-Normal
## Family: poisson
## No. of species: 101
## Total abundance: 505
##
## log.mu log.sigma Deviance AIC BIC
## 0.951926 1.165929 17.077549 317.656487 322.886728
Plot lognormal
plot(mod)
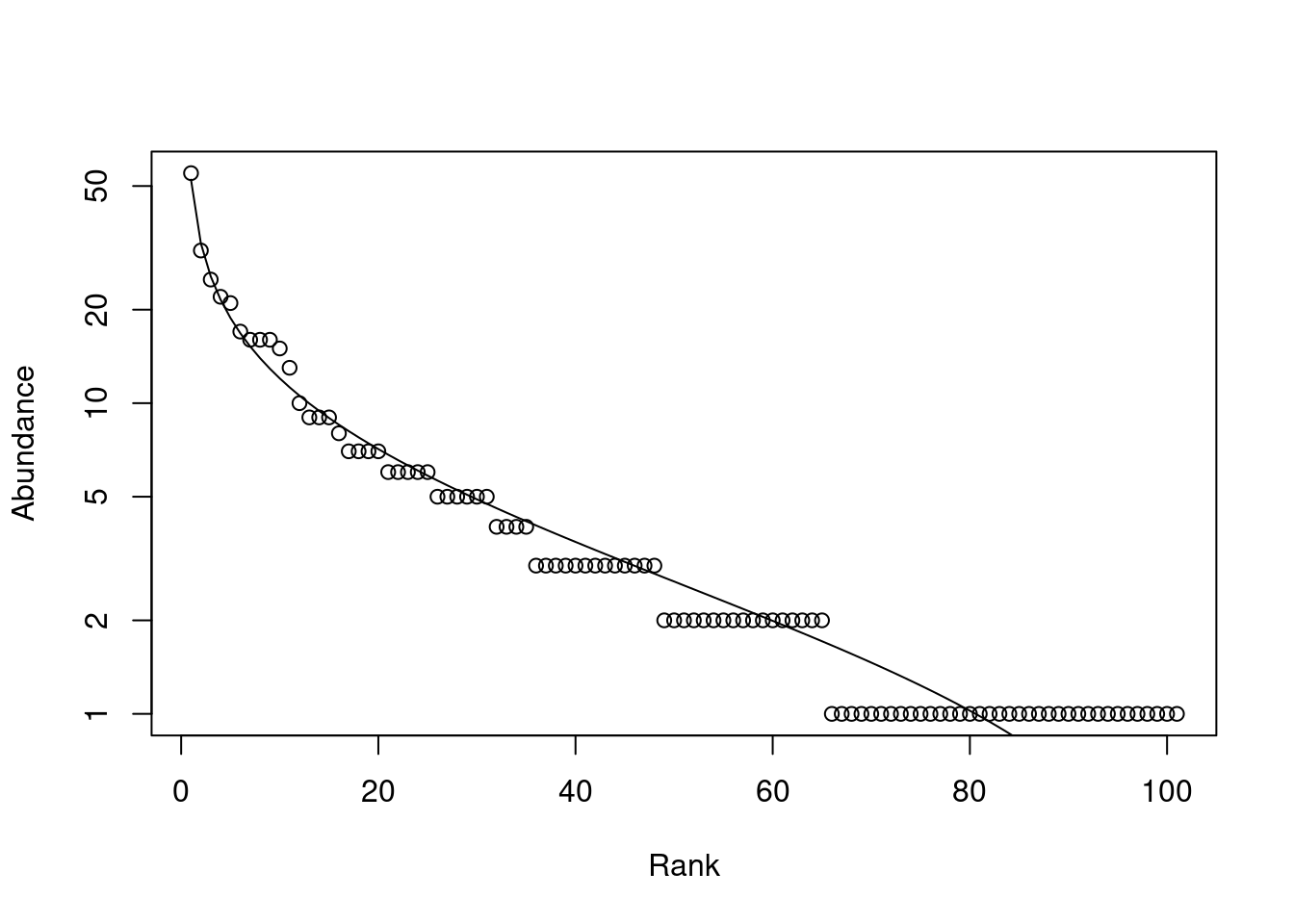
Código para vários modelos
mod2 <- radfit(BCI[1,])
mod2
##
## RAD models, family poisson
## No. of species 93, total abundance 448
##
## par1 par2 par3 Deviance AIC BIC
## Null 39.5261 315.4362 315.4362
## Preemption 0.042797 21.8939 299.8041 302.3367
## Lognormal 1.0687 1.0186 25.1528 305.0629 310.1281
## Zipf 0.11033 -0.74705 61.0465 340.9567 346.0219
## Mandelbrot 100.52 -2.312 24.084 4.2271 286.1372 293.7350
Plot com vários modelos
plot(mod2)
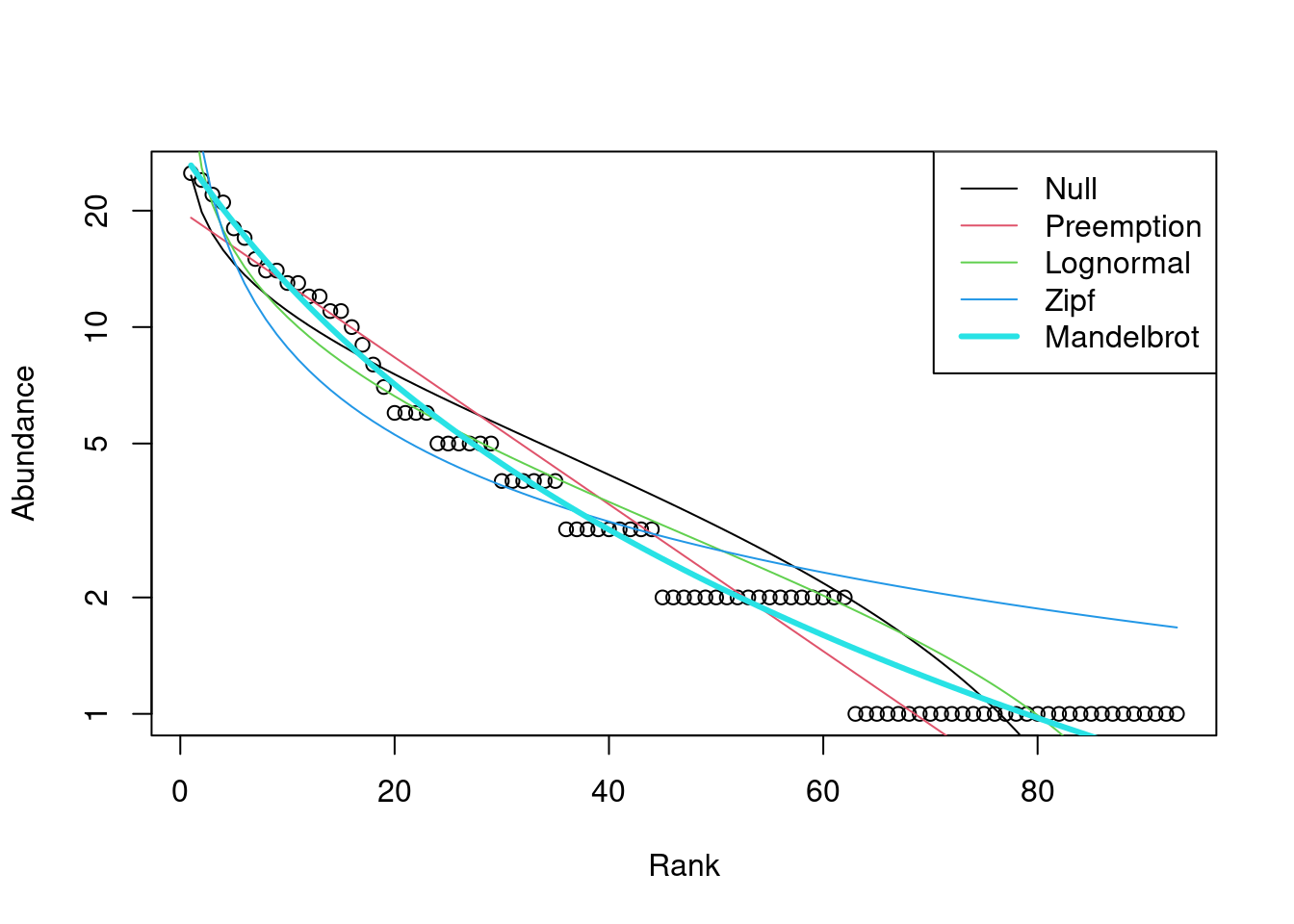
OUtro pacote, o “BiodiversityR” é muito interessante e traz suas funções úteis
Código
data(dune)
data("dune.env")
bio<-rankabuncomp(dune, dune.env, factor='Management', return.data=TRUE, specnames=c(1:2), legend=FALSE)
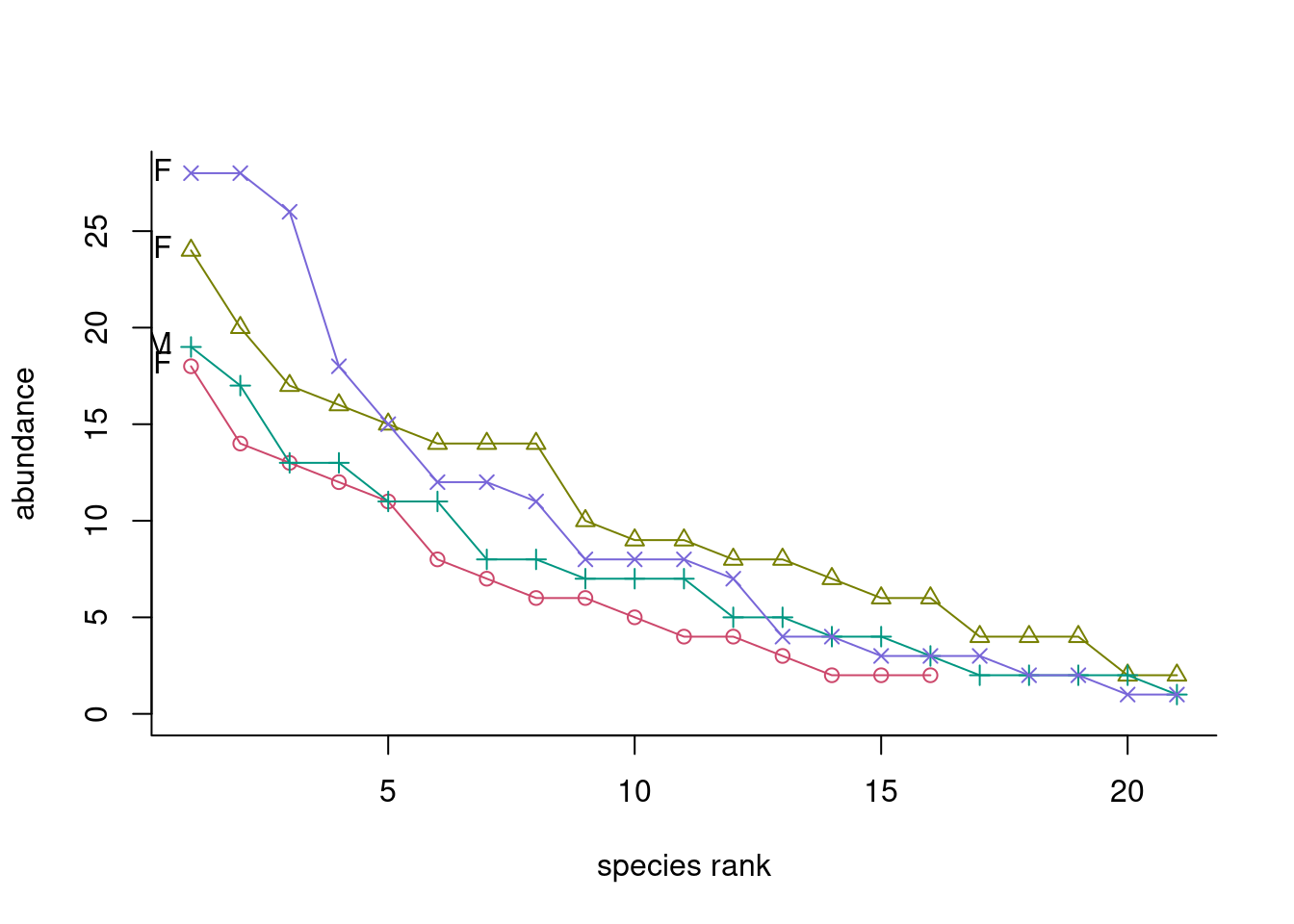
bio
## Grouping species labelit rank abundance proportion plower pupper accumfreq
## 1 BF Lolipere TRUE 1 18 15.4 3.6 27.2 15.4
## 2 BF Trifrepe TRUE 2 14 12.0 6.6 17.3 27.4
## 3 BF Scorautu FALSE 3 13 11.1 0.7 21.5 38.5
## 4 BF Poaprat FALSE 4 12 10.3 6.3 14.2 48.7
## 5 BF Poatriv FALSE 5 11 9.4 -9.9 28.7 58.1
## 6 BF Bromhord FALSE 6 8 6.8 -5.2 18.9 65.0
## 7 BF Achimill FALSE 7 7 6.0 -5.0 17.0 70.9
## 8 BF Planlanc FALSE 8 6 5.1 -6.9 17.1 76.1
## 9 BF Bracruta FALSE 9 6 5.1 -9.3 19.5 81.2
## 10 BF Bellpere FALSE 10 5 4.3 -4.0 12.5 85.5
## 11 BF Anthodor FALSE 11 4 3.4 -10.6 17.4 88.9
## 12 BF Elymrepe FALSE 12 4 3.4 -10.8 17.6 92.3
## 13 BF Vicilath FALSE 13 3 2.6 -4.6 9.8 94.9
## 14 BF Alopgeni FALSE 14 2 1.7 -5.4 8.8 96.6
## 15 BF Hyporadi FALSE 15 2 1.7 -6.3 9.7 98.3
## 16 BF Sagiproc FALSE 16 2 1.7 -6.3 9.7 100.0
## 17 HF Poatriv TRUE 1 24 11.3 8.4 14.1 11.3
## 18 HF Lolipere TRUE 2 20 9.4 3.7 15.1 20.7
## 19 HF Poaprat FALSE 3 17 8.0 4.9 11.1 28.6
## 20 HF Rumeacet FALSE 4 16 7.5 1.1 13.9 36.2
## 21 HF Planlanc FALSE 5 15 7.0 -0.7 14.7 43.2
## 22 HF Scorautu FALSE 6 14 6.6 5.2 8.0 49.8
## 23 HF Trifrepe FALSE 7 14 6.6 3.3 9.8 56.3
## 24 HF Bracruta FALSE 8 14 6.6 1.9 11.2 62.9
## 25 HF Elymrepe FALSE 9 10 4.7 -3.6 13.0 67.6
## 26 HF Anthodor FALSE 10 9 4.2 -0.8 9.2 71.8
## 27 HF Trifprat FALSE 11 9 4.2 -1.4 9.9 76.1
## 28 HF Alopgeni FALSE 12 8 3.8 -3.1 10.6 79.8
## 29 HF Juncarti FALSE 13 8 3.8 -2.8 10.3 83.6
## 30 HF Agrostol FALSE 14 7 3.3 -2.6 9.1 86.9
## 31 HF Achimill FALSE 15 6 2.8 -0.3 5.9 89.7
## 32 HF Juncbufo FALSE 16 6 2.8 -2.5 8.1 92.5
## 33 HF Eleopalu FALSE 17 4 1.9 -3.4 7.2 94.4
## 34 HF Sagiproc FALSE 18 4 1.9 -1.4 5.2 96.2
## 35 HF Bromhord FALSE 19 4 1.9 -1.4 5.1 98.1
## 36 HF Bellpere FALSE 20 2 0.9 -1.7 3.5 99.1
## 37 HF Ranuflam FALSE 21 2 0.9 -1.7 3.6 100.0
## 38 NM Scorautu TRUE 1 19 12.6 6.0 19.2 12.6
## 39 NM Bracruta TRUE 2 17 11.3 2.6 19.9 23.8
## 40 NM Agrostol FALSE 3 13 8.6 -1.2 18.4 32.5
## 41 NM Eleopalu FALSE 4 13 8.6 -1.4 18.6 41.1
## 42 NM Salirepe FALSE 5 11 7.3 -0.2 14.8 48.3
## 43 NM Trifrepe FALSE 6 11 7.3 -2.0 16.6 55.6
## 44 NM Anthodor FALSE 7 8 5.3 -3.8 14.4 60.9
## 45 NM Ranuflam FALSE 8 8 5.3 -1.2 11.8 66.2
## 46 NM Hyporadi FALSE 9 7 4.6 -3.8 13.1 70.9
## 47 NM Juncarti FALSE 10 7 4.6 -2.7 12.0 75.5
## 48 NM Callcusp FALSE 11 7 4.6 -2.8 12.1 80.1
## 49 NM Airaprae FALSE 12 5 3.3 -2.4 9.0 83.4
## 50 NM Planlanc FALSE 13 5 3.3 -2.6 9.2 86.8
## 51 NM Poaprat FALSE 14 4 2.6 -2.5 7.8 89.4
## 52 NM Comapalu FALSE 15 4 2.6 -1.8 7.1 92.1
## 53 NM Sagiproc FALSE 16 3 2.0 -2.9 6.9 94.0
## 54 NM Achimill FALSE 17 2 1.3 -2.4 5.0 95.4
## 55 NM Bellpere FALSE 18 2 1.3 -2.0 4.7 96.7
## 56 NM Empenigr FALSE 19 2 1.3 -1.9 4.6 98.0
## 57 NM Lolipere FALSE 20 2 1.3 -2.0 4.7 99.3
## 58 NM Vicilath FALSE 21 1 0.7 -1.0 2.3 100.0
## 59 SF Agrostol TRUE 1 28 13.7 7.8 19.7 13.7
## 60 SF Poatriv TRUE 2 28 13.7 6.3 21.1 27.5
## 61 SF Alopgeni FALSE 3 26 12.7 4.5 21.0 40.2
## 62 SF Lolipere FALSE 4 18 8.8 -2.1 19.8 49.0
## 63 SF Poaprat FALSE 5 15 7.4 0.5 14.2 56.4
## 64 SF Elymrepe FALSE 6 12 5.9 -1.0 12.8 62.3
## 65 SF Bracruta FALSE 7 12 5.9 0.8 10.9 68.1
## 66 SF Sagiproc FALSE 8 11 5.4 -0.8 11.5 73.5
## 67 SF Eleopalu FALSE 9 8 3.9 -6.3 14.1 77.5
## 68 SF Scorautu FALSE 10 8 3.9 1.4 6.4 81.4
## 69 SF Trifrepe FALSE 11 8 3.9 0.5 7.3 85.3
## 70 SF Juncbufo FALSE 12 7 3.4 -2.3 9.2 88.7
## 71 SF Bellpere FALSE 13 4 2.0 -0.9 4.8 90.7
## 72 SF Ranuflam FALSE 14 4 2.0 -1.3 5.2 92.6
## 73 SF Juncarti FALSE 15 3 1.5 -2.4 5.3 94.1
## 74 SF Callcusp FALSE 16 3 1.5 -2.4 5.3 95.6
## 75 SF Bromhord FALSE 17 3 1.5 -2.1 5.0 97.1
## 76 SF Rumeacet FALSE 18 2 1.0 -1.5 3.5 98.0
## 77 SF Cirsarve FALSE 19 2 1.0 -1.4 3.3 99.0
## 78 SF Achimill FALSE 20 1 0.5 -0.9 1.9 99.5
## 79 SF Chenalbu FALSE 21 1 0.5 -0.8 1.8 100.0
## logabun rankfreq
## 1 1.3 6.2
## 2 1.1 12.5
## 3 1.1 18.8
## 4 1.1 25.0
## 5 1.0 31.2
## 6 0.9 37.5
## 7 0.8 43.8
## 8 0.8 50.0
## 9 0.8 56.2
## 10 0.7 62.5
## 11 0.6 68.8
## 12 0.6 75.0
## 13 0.5 81.2
## 14 0.3 87.5
## 15 0.3 93.8
## 16 0.3 100.0
## 17 1.4 4.8
## 18 1.3 9.5
## 19 1.2 14.3
## 20 1.2 19.0
## 21 1.2 23.8
## 22 1.1 28.6
## 23 1.1 33.3
## 24 1.1 38.1
## 25 1.0 42.9
## 26 1.0 47.6
## 27 1.0 52.4
## 28 0.9 57.1
## 29 0.9 61.9
## 30 0.8 66.7
## 31 0.8 71.4
## 32 0.8 76.2
## 33 0.6 81.0
## 34 0.6 85.7
## 35 0.6 90.5
## 36 0.3 95.2
## 37 0.3 100.0
## 38 1.3 4.8
## 39 1.2 9.5
## 40 1.1 14.3
## 41 1.1 19.0
## 42 1.0 23.8
## 43 1.0 28.6
## 44 0.9 33.3
## 45 0.9 38.1
## 46 0.8 42.9
## 47 0.8 47.6
## 48 0.8 52.4
## 49 0.7 57.1
## 50 0.7 61.9
## 51 0.6 66.7
## 52 0.6 71.4
## 53 0.5 76.2
## 54 0.3 81.0
## 55 0.3 85.7
## 56 0.3 90.5
## 57 0.3 95.2
## 58 0.0 100.0
## 59 1.4 4.8
## 60 1.4 9.5
## 61 1.4 14.3
## 62 1.3 19.0
## 63 1.2 23.8
## 64 1.1 28.6
## 65 1.1 33.3
## 66 1.0 38.1
## 67 0.9 42.9
## 68 0.9 47.6
## 69 0.9 52.4
## 70 0.8 57.1
## 71 0.6 61.9
## 72 0.6 66.7
## 73 0.5 71.4
## 74 0.5 76.2
## 75 0.5 81.0
## 76 0.3 85.7
## 77 0.3 90.5
## 78 0.0 95.2
## 79 0.0 100.0
Plot (com ggplot)
library(ggplot2)
library(ggrepel)
plotgg1 <- ggplot(data=bio, aes(x = rank, y = abundance)) +
scale_x_continuous(expand=c(0, 1), sec.axis = dup_axis(labels=NULL, name=NULL)) +
scale_y_continuous(expand=c(0, 1), sec.axis = dup_axis(labels=NULL, name=NULL)) +
geom_line(aes(colour=Grouping), size=1) +
geom_point(aes(colour=Grouping, shape=Grouping), size=5, alpha=0.7) +
geom_text_repel(data=subset(bio, labelit == TRUE),
aes(colour=Grouping, label=species),
angle=45, nudge_x=1, nudge_y=1, show.legend=FALSE) +
scale_color_brewer(palette = "Set1") +
labs(x = "rank", y = "abundance", colour = "Management", shape = "Management")
## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.
plotgg1
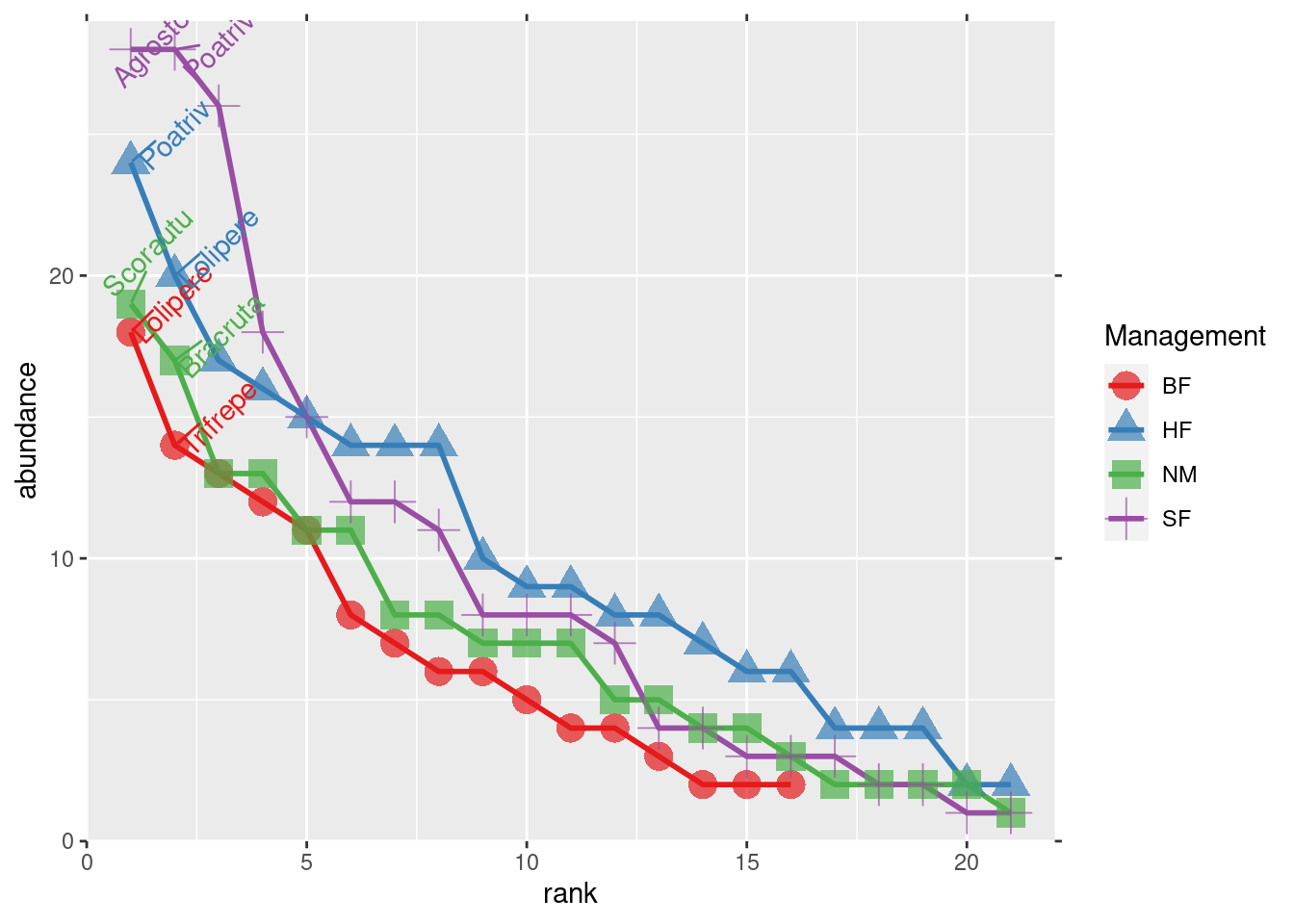
RA.data <- rankabuncomp(dune, y=dune.env, factor='Management',
return.data=TRUE, specnames=c(1:10), legend=FALSE)
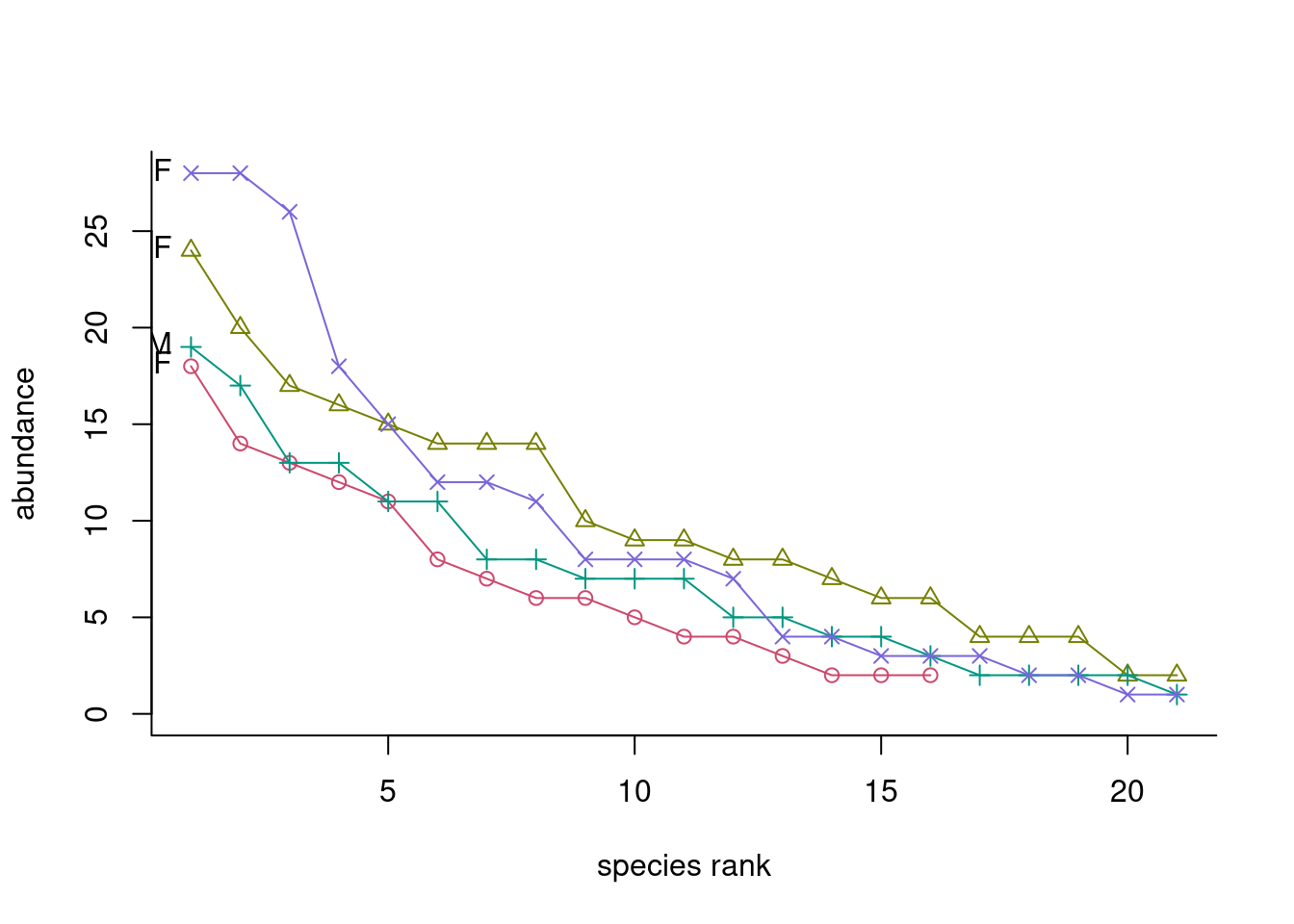
plotgg2 <- ggplot(data=RA.data, aes(x = rank, y = abundance)) +
scale_x_continuous(expand=c(0, 1), sec.axis = dup_axis(labels=NULL, name=NULL)) +
scale_y_continuous(expand=c(0, 1), sec.axis = dup_axis(labels=NULL, name=NULL)) +
geom_line(aes(colour=Grouping), size=1) +
geom_point(aes(colour=Grouping), size=5, alpha=0.7) +
geom_text_repel(data=subset(RA.data, labelit == TRUE),
aes(label=species),
angle=45, nudge_x=1, nudge_y=1, show.legend=FALSE) +
scale_color_brewer(palette = "Set1") +
facet_wrap(~ Grouping) +
labs(x = "rank", y = "abundance", colour = "Management")
plotgg2
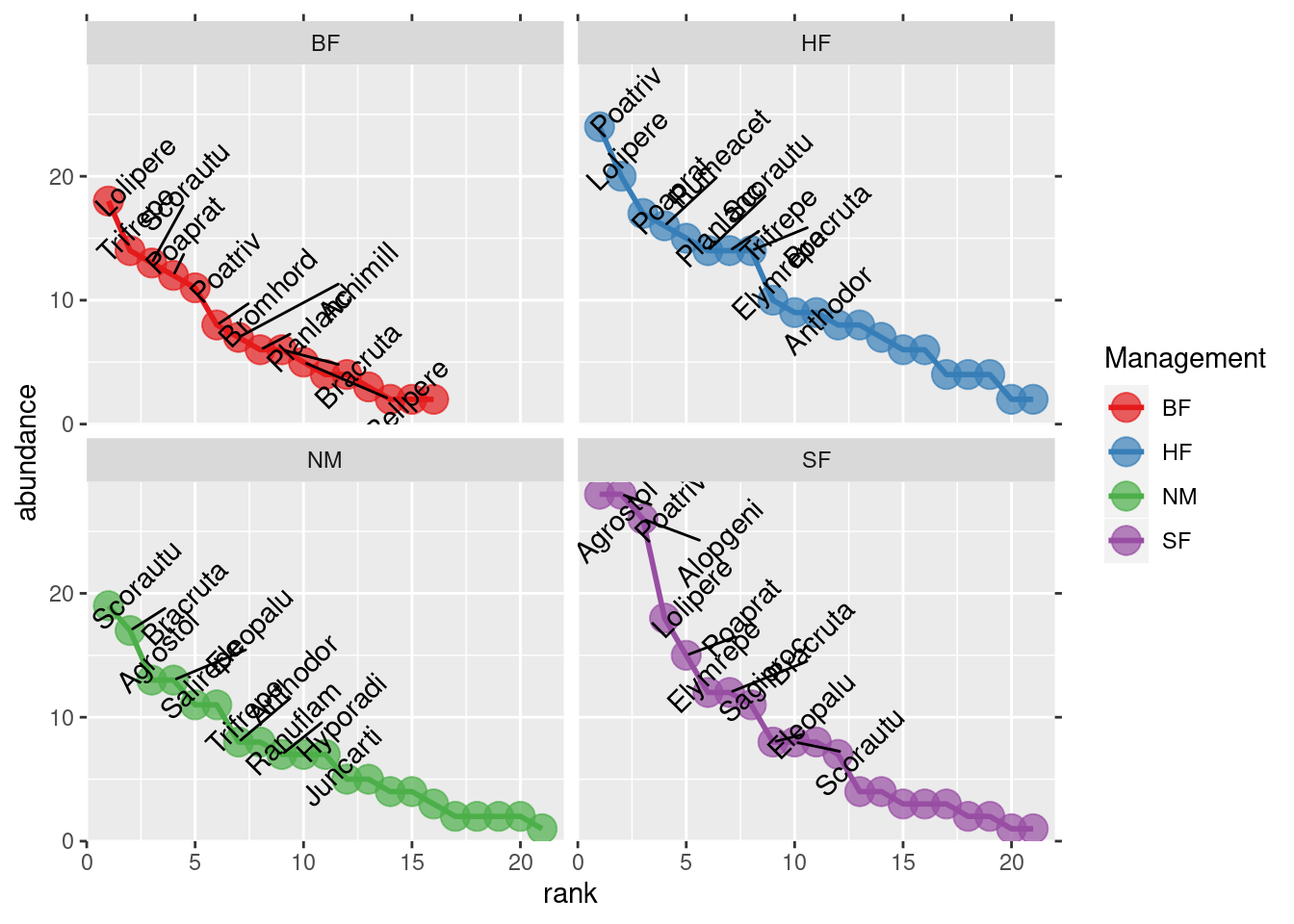
Exercício
- Faça uma análise descritiva dessa da nossa base de dados de comunidade culinária usando esses códigos.
- Utilize funções prontas dos pacotes mas também tente chegar so resultados esperados com funções básicas do R
- Comente suas análises dando uma interpretação ecológica aos gráficos, crie grpaficos!!