Modules Ecologia Numérica Medidas de diversidade verdadeira
Medidas de diversidade verdadeira

Texto extraído do livro Análises Ecológicas no R (in press)
Desafios da mensuração da diversidade verdadeira
Números de Hill ou Série de Hill Embora os índices de Shannon-Wiener e Gini-Simpson sejam amplamente usados em estudos ecológicos e de conservação, eles sofrem de propriedades matemáticas e não representam a diversidade propriamente dita (L. Jost 2006). Portanto, quando o objetivo é avaliar a diversidade, os índices de Shannon-Wiener e Gini-Simpson não deveriam ser utilizados na sua forma padrão, mas transformados em números efetivos de espécies ou diversidade verdadeira (L. Jost 2006). O número efetivo de espécies é o número de espécies igualmente abundantes (i.e. todas as espécies com a mesma abundância) necessárias para produzir o valor observado para um determinado índice. Por exemplo, uma comunidade com índice de Shannon-Wiener estimado de 4,5 teria um número efetivo de 90 espécies igualmente abundantes. Jost et al. (2006) usam o seguinte exemplo para explicar o conceito do número efetivo de espécies - uma comunidade com 16 espécies igualmente abundantes é duas vezes mais diversa do que uma comunidade com 8 espécies igualmente abundantes. Neste caso, a diversidade deveria ser proporcional ao número de espécies. Contudo, quando aplicamos os índices de diversidade para estas comunidades com 16 e 8 espécies (cada espécie com 5 indivíduos), o índice de Shannon-Wiener é 2,772 e 2,079, respectivamente, e o índice de Gini-Simpson é 0,937 e 0,875, respectivamente. Claramente, os valores estimados pelos índices de diversidade não representam a diferença entre as comunidades porque eles carecem de uma particularidade matemática conhecida como propriedade de duplicação.
O próximo exemplo (modificado do website de Lou Jost; http://www.loujost.com/), demostra a importância da transformação dos índices de diversidade em números efetivos de espécies. Imagine que você foi contratado para avaliar a diversidade de peixes em um riacho antes e depois da instalação de uma usina hidrelétrica. Suponha que os valores estimados pelo índice de Gini-Simpson foi de 0,99 antes da instalação e de 0,97 depois da instalação. A princípio, você poderia concluir que a diversidade diminuiu somente 2% e que a instalação da hidrelétrica não afetou a diversidade de peixes no riacho. Contudo, transformando os valores do índice de diversidade em números efetivos, percebemos que antes da instalação a diversidade do riacho equivale a 100 espécies igualmente abundantes, enquanto após a instalação, a diversidade equivale a 33 espécies igualmente abundantes. Portanto, a queda da diversidade foi de 66% e não 2%.
Hill (1973) derivou uma equação geral para o cálculo do número efetivo de espécies ou diversidade verdadeira que depende apenas do valor de q e da abundância relativa das espécies.

Onde:
q = é um parâmetro conhecido como ordem da diversidade e é usado para dar peso às espécies comuns ou raras. q = 0 não considera a frequência das espécies e representa a riqueza observada de espécies, q = 1 equivale a transformação do índice de Shannon-Wiener (i.e. exp(H’)) e atribui pesos às espécies com base na proporção das suas frequências e, q = 2 equivale à transformação do índice de Gini-Simpson (i.e. 1/(1-D)) e atribui peso às espécies mais comuns. Valores de q <1 favorecem espécies raras, enquanto valores de q > 1 favorecem espécies comuns.
pi = abundância relativa de cada espécie, calculada pela proporção dos indivíduos de uma espécie pelo número total dos indivíduos na comunidade
Vamos calcular o Número de Hill para as comunidades do nosso exemplo.
Calculando o Número de Hill com q = 0.
library(devtools)
## Carregando pacotes exigidos: usethis
##
## Attaching package: 'devtools'
## The following object is masked from 'package:permute':
##
## check
library(ecodados)
library (vegan)
library(ggplot2)
library(BiodiversityR)
## Carregando pacotes exigidos: tcltk
## BiodiversityR 2.14-4: Use command BiodiversityRGUI() to launch the Graphical User Interface;
## to see changes use BiodiversityRGUI(changeLog=TRUE, backward.compatibility.messages=TRUE)
library(hillR)
## Dados
composicao_especies <- ecodados::composicao_anuros_div_taxonomica
precipitacao <- ecodados::precipitacao_div_taxonomica
hill_res_q_0 <- hill_taxa(composicao_especies, q = 0)
hill_res_q_0
## Com_1 Com_2 Com_3 Com_4 Com_5 Com_6 Com_7 Com_8 Com_9 Com_10
## 10 10 5 5 5 6 2 4 6 4
Número de Hill para q = 1
hill_res_q_1 <- hill_taxa(composicao_especies, q = 1)
hill_res_q_1
## Com_1 Com_2 Com_3 Com_4 Com_5 Com_6 Com_7 Com_8
## 10.000000 1.649196 2.606507 4.987156 4.420220 4.762172 2.000000 3.021912
## Com_9 Com_10
## 5.551608 3.538328
Número de Hill para q = 2
hill_res_q_2 <- hill_taxa(composicao_especies, q = 2)
hill_res_q_2
## Com_1 Com_2 Com_3 Com_4 Com_5 Com_6 Com_7 Com_8
## 10.000000 1.206273 1.928571 4.974223 4.145078 4.300813 2.000000 2.409639
## Com_9 Com_10
## 5.232558 3.270270
Resultados
res_hill <- data.frame(hill_res_q_0, hill_res_q_1, hill_res_q_2)
colnames(res_hill) <- c("q=0", "q=1", "q=2")
head(res_hill)
## q=0 q=1 q=2
## Com_1 10 10.000000 10.000000
## Com_2 10 1.649196 1.206273
## Com_3 5 2.606507 1.928571
## Com_4 5 4.987156 4.974223
## Com_5 5 4.420220 4.145078
## Com_6 6 4.762172 4.300813
Interpretação dos resultados
Como na comunidade 1 todas as espécies são igualmente abundantes, alterar os valores de q não altera o número efetivo de espécies que permanece sempre 10. Contudo, na comunidade 2, que apresenta alta dominância de uma espécie, alterar os valores de q diminui consideravelmente a estimativa da diversidade. A vantagem dos Números de Hill é que eles são de fácil interpretação e comparação entre as comunidades. Fator ausente para os índices de diversidade.
Exercício
- Reproduza as análises acima com a base do BCI ou Outra base à sua escolha
- Grafique os resutados num “diversity profile”
- Tente interpretar os resultados
Exemplo simples para você substituir com os dados de BCI
(df <- data.frame(C1 = c(10, 10, 10, 10), C2 = c(0, 20, 35, 5), C3 = c(25, 15, 0, 2), row.names = c("sp1", "sp2", "sp3", "sp4")))
## C1 C2 C3
## sp1 10 0 25
## sp2 10 20 15
## sp3 10 35 0
## sp4 10 5 2
library(entropart)
mc<-MetaCommunity(df)
plot(mc)
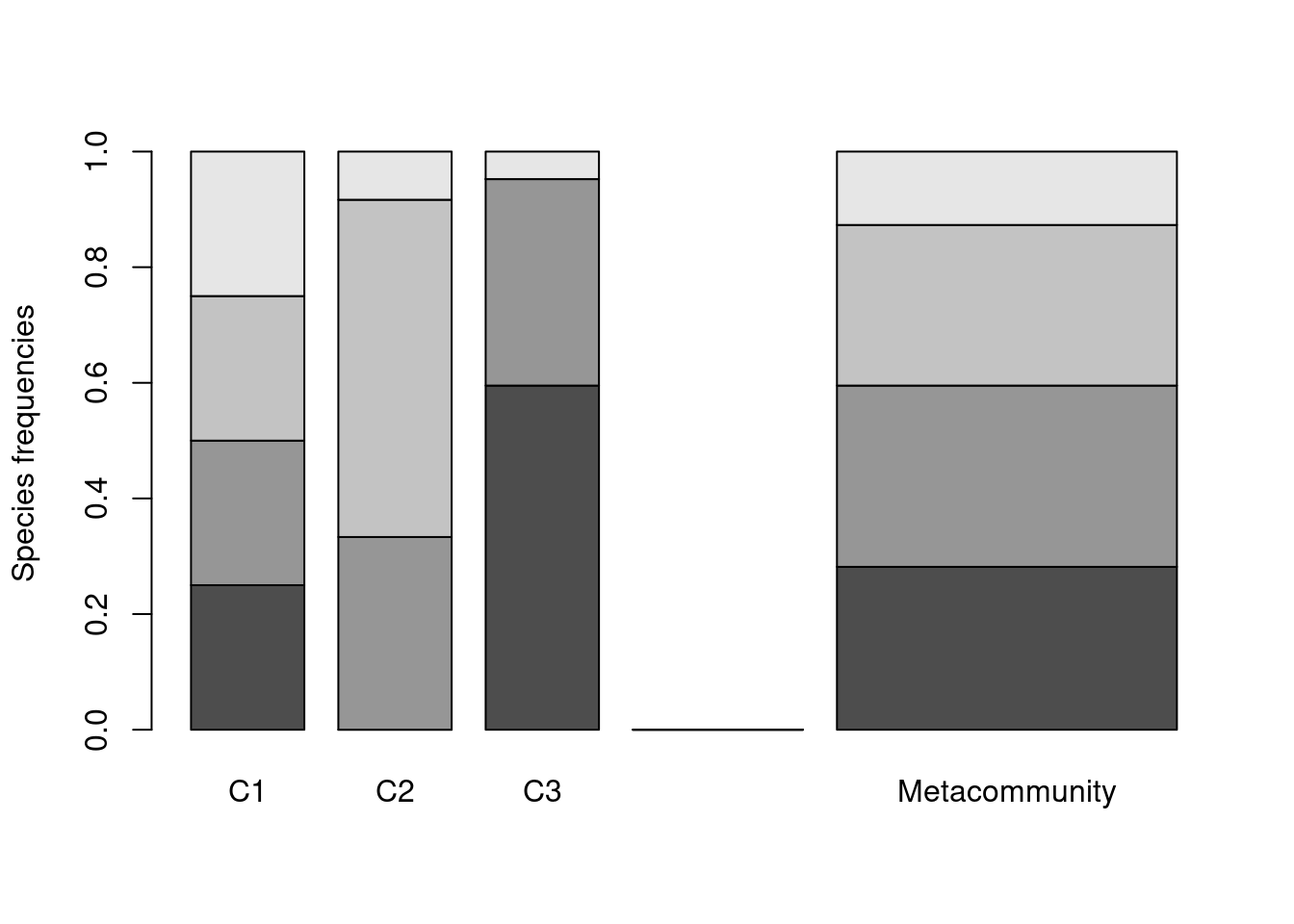
summary(DivPart(q=0, mc), Correction="None")
## HCDT diversity partitioning of order 0 of metaCommunity mc
##
## Alpha diversity of communities:
## C1 C2 C3
## 4 3 3
## Total alpha diversity of the communities:
## [1] 3.333333
## Beta diversity of the communities:
## None
## 1.2
## Gamma diversity of the metacommunity:
## None
## 4
summary(DivPart(q=1, mc), Correction="None")
## HCDT diversity partitioning of order 1 of metaCommunity mc
##
## Alpha diversity of communities:
## C1 C2 C3
## 4.000000 2.429521 2.273918
## Total alpha diversity of the communities:
## [1] 2.806199
## Beta diversity of the communities:
## None
## 1.358779
## Gamma diversity of the metacommunity:
## None
## 3.813005
summary(DivPart(q=2, mc), Correction="None")
## HCDT diversity partitioning of order 2 of metaCommunity mc
##
## Alpha diversity of communities:
## C1 C2 C3
## 4.000000 2.181818 2.065574
## Total alpha diversity of the communities:
## [1] 2.515807
## Beta diversity of the communities:
## None
## 1.467046
## Gamma diversity of the metacommunity:
## None
## 3.690806
autoplot(DivProfile(q.seq = seq(0, 2, 0.1),MC=mc, Correction = "None"))
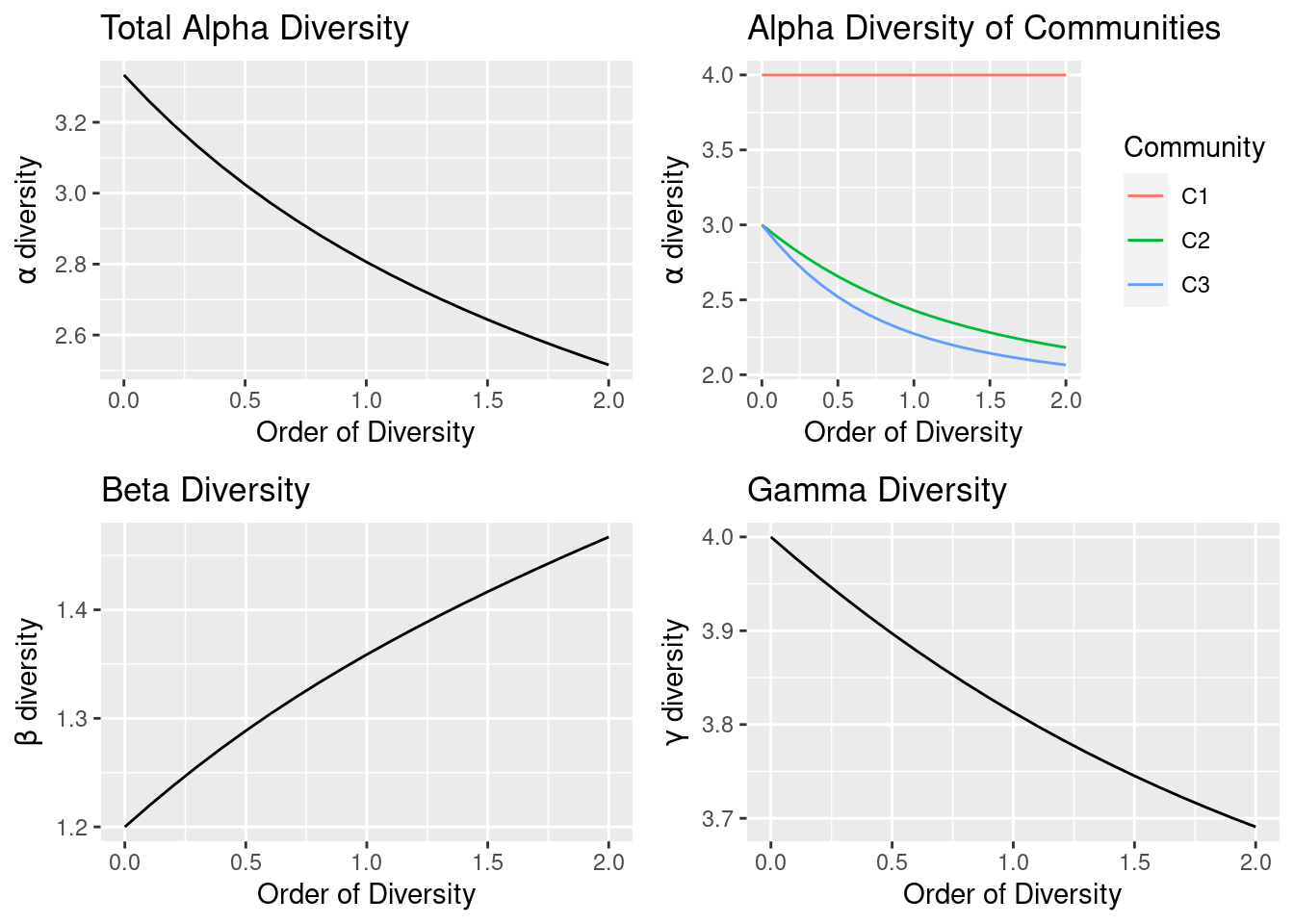
# Tem mais coisa que pode ser explorada
# Estimadores de diversidade
alfa.est0<-DivEst(q = 0, mc, Simulations = 100, Correction = "None")
plot(alfa.est0)
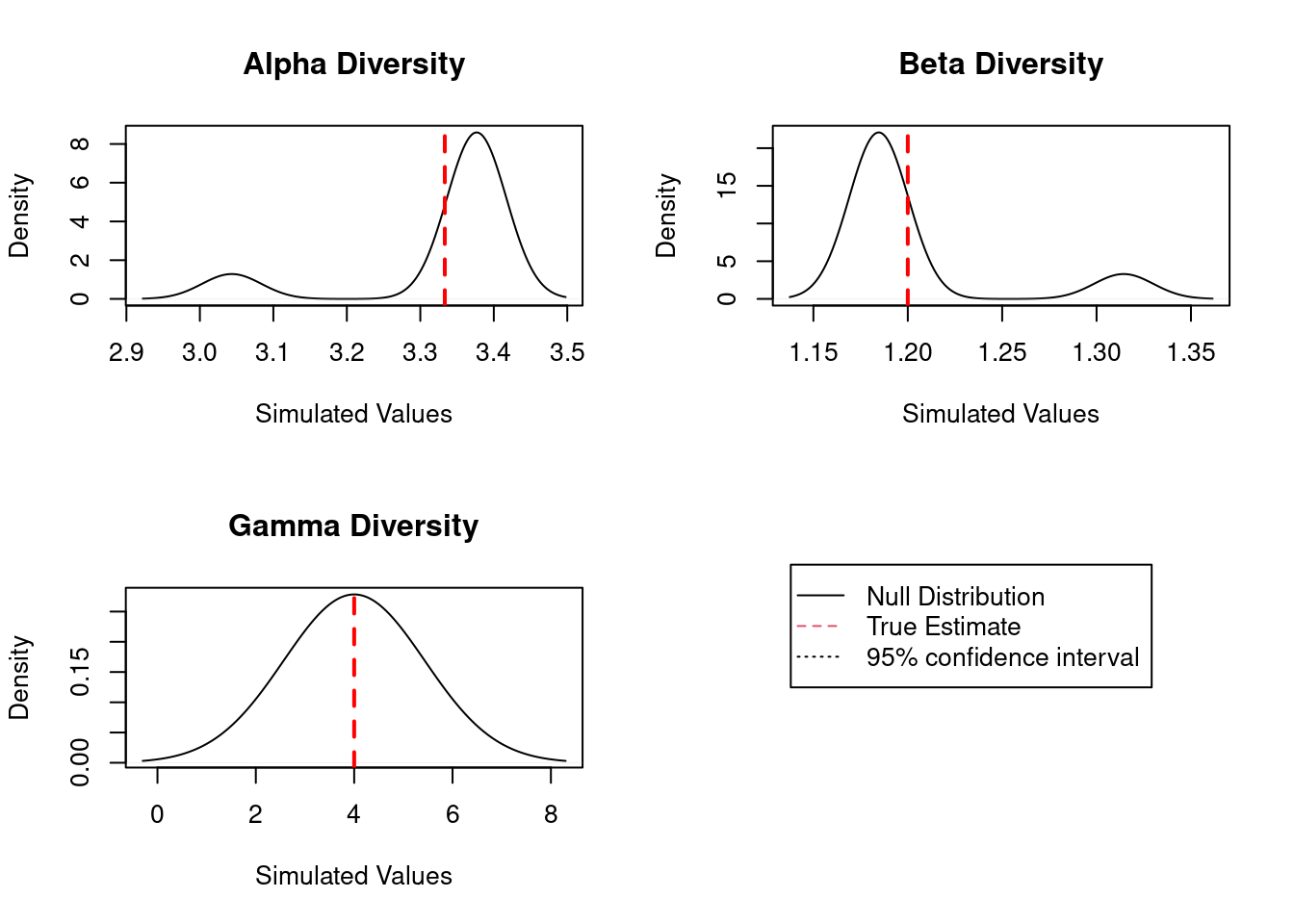
alfa.est1<-DivEst(q = 1, mc, Simulations = 100, Correction = "None")
plot(alfa.est1)
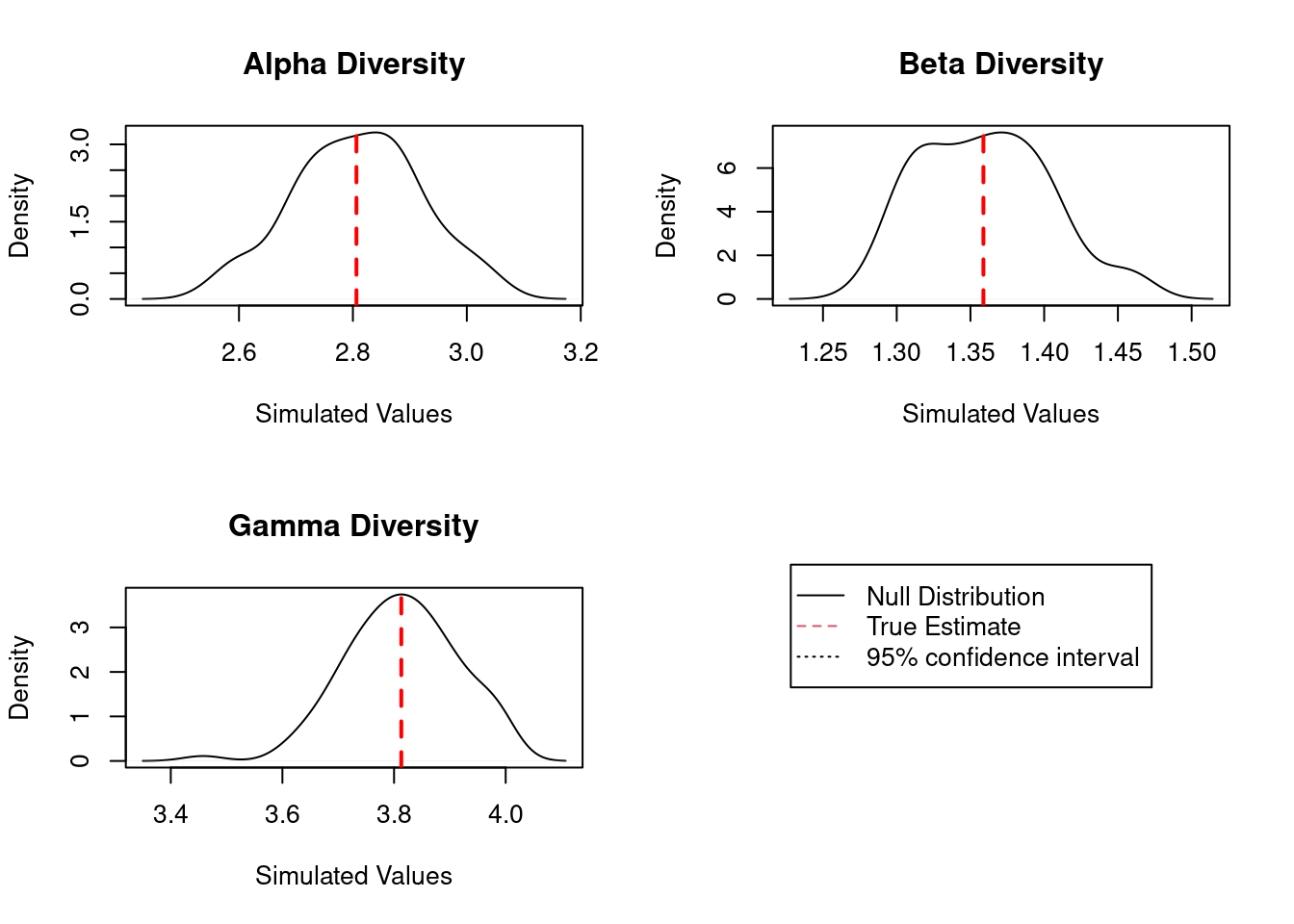
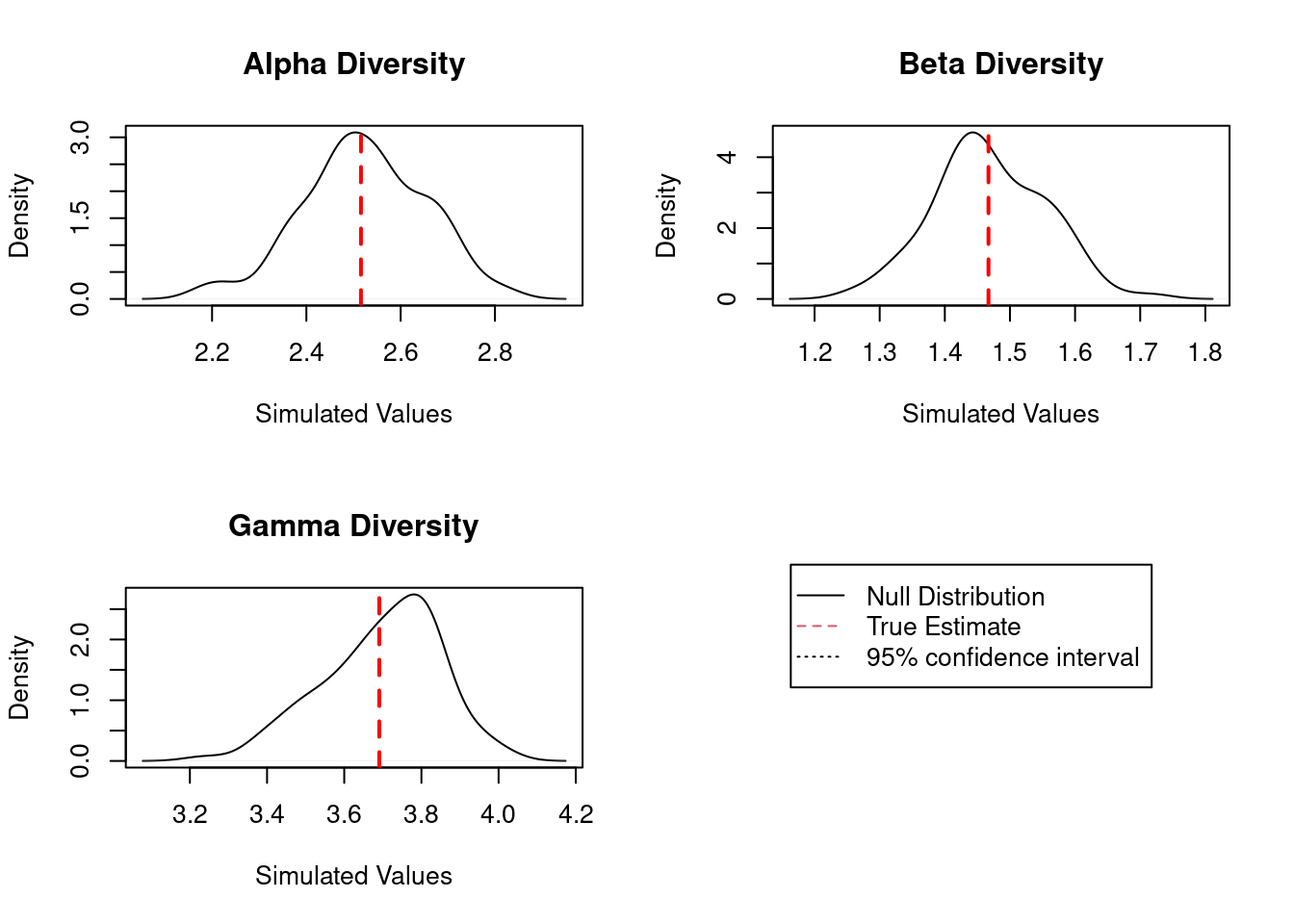
alfa.est2<-DivEst(q = 2, mc, Simulations = 100, Correction = "None")
plot(alfa.est2)