Modules Ecologia Numérica Medidas de Associação
Medidas de Associação
Na ecologia usamos muitas medidas que fazem uma ligação entre pares de dados. Esses pares de dados podem ser espécies, ou locais de coleta. Há uma enorme variedade de métricas que vão nos oferecer uma medida de associação entre pares. Essas medidas são reportadas na forma de índices ou métricas que têm naturezas distintas, mas todas tem a particularidade de gerar uma matriz quadrada e simétrica de dimensões n x n quando se comparam objetos ou p x p quando se comparam variáveis (as letras são conveções). Essas matrizes de assossiação serão criadas e facilmente pelas análises, mas o pesquisador aqui tem um papel fundamental: escolher as métricas
Q mode & R mode
Como de constume, vamos seguir nessa disciplina o roteiro proposto pelo livro texto Numerical Ecology with R.
Novamente, isso é uma convenção para distinguir as comparações entre objetos Q-mode ou variáveis R-mode. As comparações entre objetos são geralmente feitas através de medidas de distância enquanto as comparações entre variáveis são realizadas com medidas de dependência.
O problema dos zeros
Todas as matrizes de dados ecológicos costumam ter zeros. Esses podem ser naturais (observações) ou simplesmente ausências de dados. Mas precisamos ter ideia de quão importantes são os zeros. No livro Numerical Ecology o exemplo dado para que entendamos os papel dos zeros em matrizes ecológicas é claro. Quando zeros são resultados de mediação de uma vairável, como concentroação de Oxigênio, a interpretação é clara, sem oxigênio, sem vida aeróbica e portanto zero frequência de vida aeróbica nessas condições é esperado. Agora, que tal se obtemos zeros em concetrações intermediárias de qualquer variável ambiental? As epécies não ocorrem aí porque tem pouco ou muito oxigênio? Note que aí temos uma interpretação diferente para cada situação. Ainda, em ambos casos a informção de ausência ou presença tem um significado ecológico, mas não sabemos as causas das ausências.

Note que as amostras A, B e C não capturaram a espécie cuja presença/abundância está representada pela linha vermelha. Portano, se essa for a única diferença entre as amostras A, B e C, os índices que não são sensíveis a este problema, não caprutam essa diferenaça e consideram que a similaridade entre A e B é igual a A e C ou B E C. Mas não é. VOcê poderia dizer porque?
praticando…
Uma boa maneira é checar se há zeros provenientes de valores vazios ou NA
load("/home/felipe/Google Drive/github/eco_numerica/data/NEwR-2ed_code_data/NEwR2-Data/Doubs.RData")
head(is.na(spe))
## Cogo Satr Phph Babl Thth Teso Chna Pato Lele Sqce Baba Albi Gogo
## 1 FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## 2 FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## 3 FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## 4 FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## 5 FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## 6 FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## Eslu Pefl Rham Legi Scer Cyca Titi Abbr Icme Gyce Ruru Blbj Alal
## 1 FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## 2 FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## 3 FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## 4 FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## 5 FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## 6 FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## Anan
## 1 FALSE
## 2 FALSE
## 3 FALSE
## 4 FALSE
## 5 FALSE
## 6 FALSE
Se os dados fossem realmente NAs então teríamos uma matriz um pouco diferente…
spe_na <- replace(spe, spe == 0, NA) # Mudei zeros por NAs
head(is.na(spe_na))
## Cogo Satr Phph Babl Thth Teso Chna Pato Lele Sqce Baba Albi Gogo Eslu
## 1 TRUE FALSE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
## 2 TRUE FALSE FALSE FALSE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
## 3 TRUE FALSE FALSE FALSE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE FALSE
## 4 TRUE FALSE FALSE FALSE TRUE TRUE TRUE TRUE TRUE FALSE TRUE TRUE FALSE FALSE
## 5 TRUE FALSE FALSE FALSE TRUE TRUE TRUE TRUE FALSE FALSE TRUE TRUE FALSE FALSE
## 6 TRUE FALSE FALSE FALSE TRUE TRUE TRUE TRUE FALSE FALSE TRUE TRUE FALSE FALSE
## Pefl Rham Legi Scer Cyca Titi Abbr Icme Gyce Ruru Blbj Alal Anan
## 1 TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
## 2 TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
## 3 TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
## 4 FALSE TRUE TRUE TRUE TRUE FALSE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
## 5 FALSE TRUE TRUE FALSE TRUE FALSE TRUE TRUE TRUE FALSE TRUE TRUE TRUE
## 6 FALSE TRUE TRUE TRUE TRUE FALSE TRUE TRUE TRUE FALSE TRUE TRUE TRUE
Nesse caso até um gráfico pode nos ajudar a ter uma dimensão da importância dos zeros NAs
image(as.matrix(spe_na))
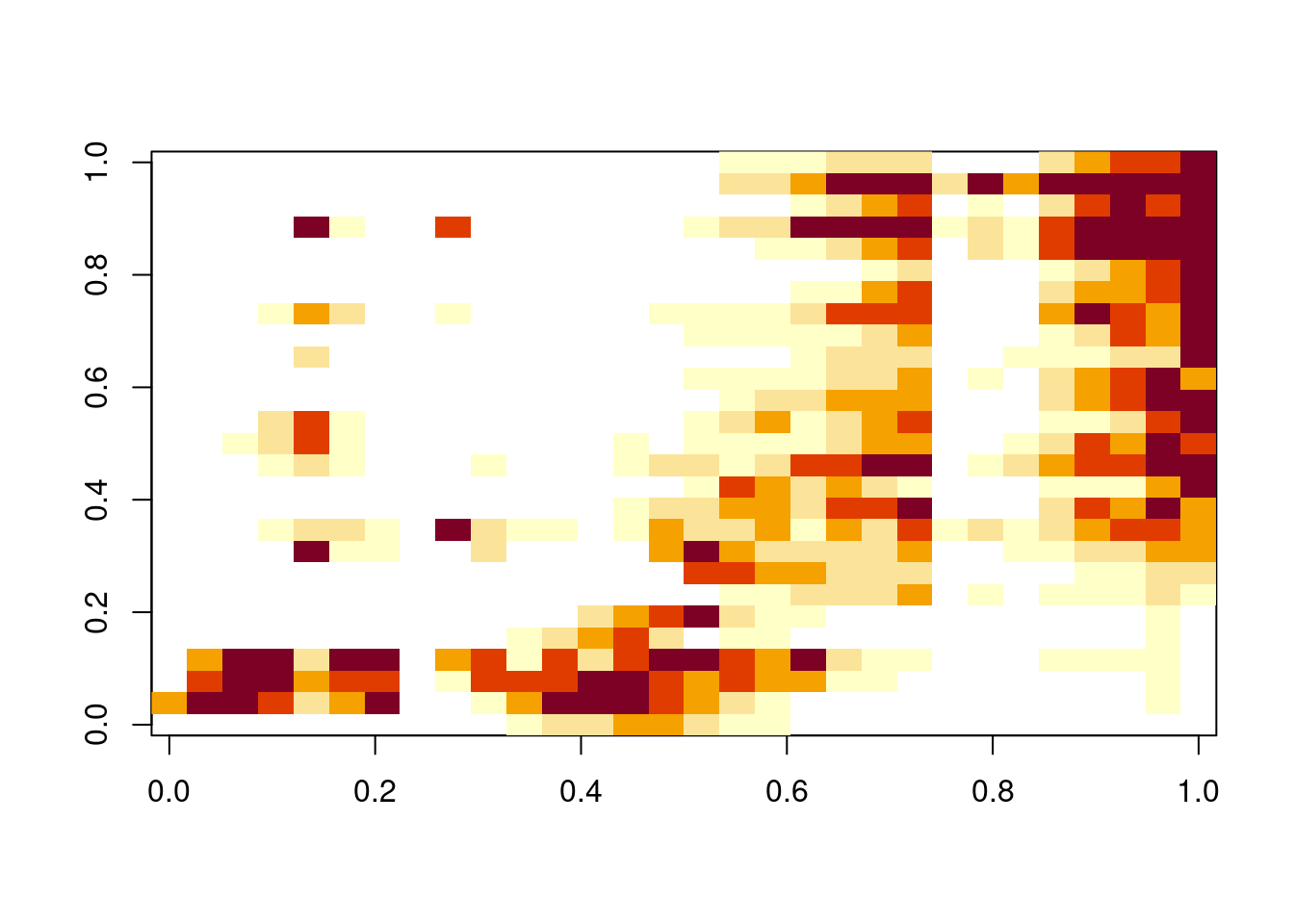
Os valores em branco são os NAs e as cores indicam as abundâncias, sendo quanto mais vermelho, mais abundante.
Perguntas para se ter em mente
- Você está comparando espécies (Q-mode) ou veriáveis ambientais (R-mode)?
- Seus dados são binários (presenças e ausências), quantitativos (medidas contínuas) ou mistos (coeficientes, categorias não binárias)?
Comparando comunidades com dados de abundância (Q-mode)
Vamos continuar usando os dados do livro Numerical Ecology with R para nossos exemplos, mas vamos mudar algumas funções de visualização.
Vamos usar os dados das espécies de peixes que já conhecemos
spe # base dos peixes da Suiça
Esses dados são quantitativos e as abundâncias variam de zero a 5 indivíduos. Como temos muitas espécies e muitas espécies raras, a escolha inicial dos índices é da família que consideramos assimétrica como o Bray-Curtis, que pode ser calculado diretamente nas abundâncias ou na base de dados transformada via funções que reduzem a diferença entre as abundâncias de espécies dominantes e raras.
só precisa fazer uma vez, depois não mais.
# Remove empty site 8
spe <- spe[-8, ]
env <- env[-8, ]
spa <- spa[-8, ]
Agora vamos comparar as medidas de dissimilaridade aplicadas
spe.db <- vegdist(spe) # method = "bray" (default)
# on log-transformed abundances
spe.dbln <- vegdist(log1p(spe))
# Chord distance matrix
spe.norm <- decostand(spe, "nor")
spe.dc <- dist(spe.norm)
# Hellinger distance matrix
spe.hel <- decostand(spe, "hel")
spe.dh <- dist(spe.hel) # Hellinger is the default distance
Exercício Q-Mode
Tente fazer uma representação gráfica de cada uma dessas matrizes com os diferentes índices e compará-la
Escreva emaicxo seus códigos e interprete os resultados escrevendo embaixo
coldiss(spe.db, diag = TRUE)
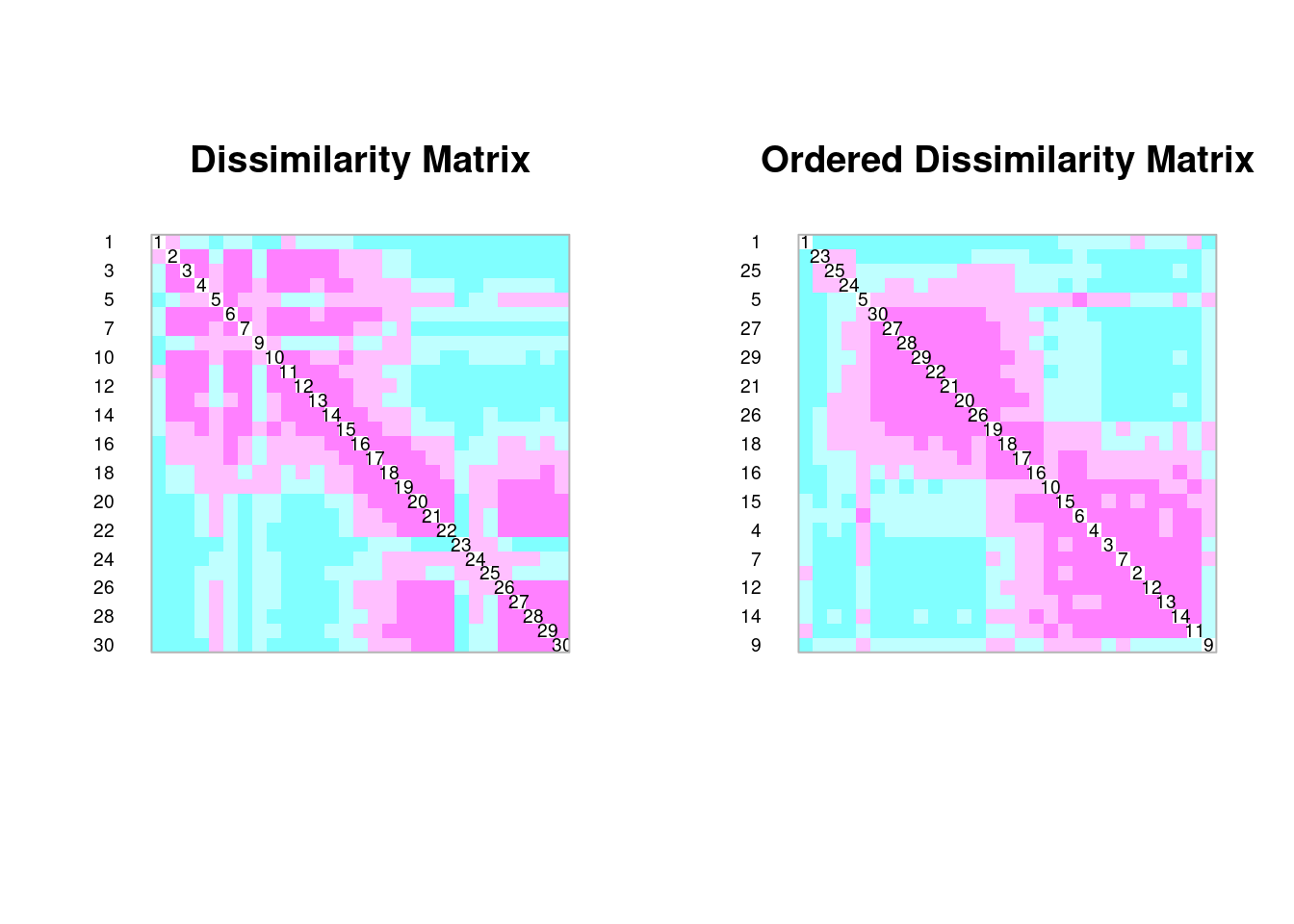
coldiss(spe.dh, diag = TRUE)
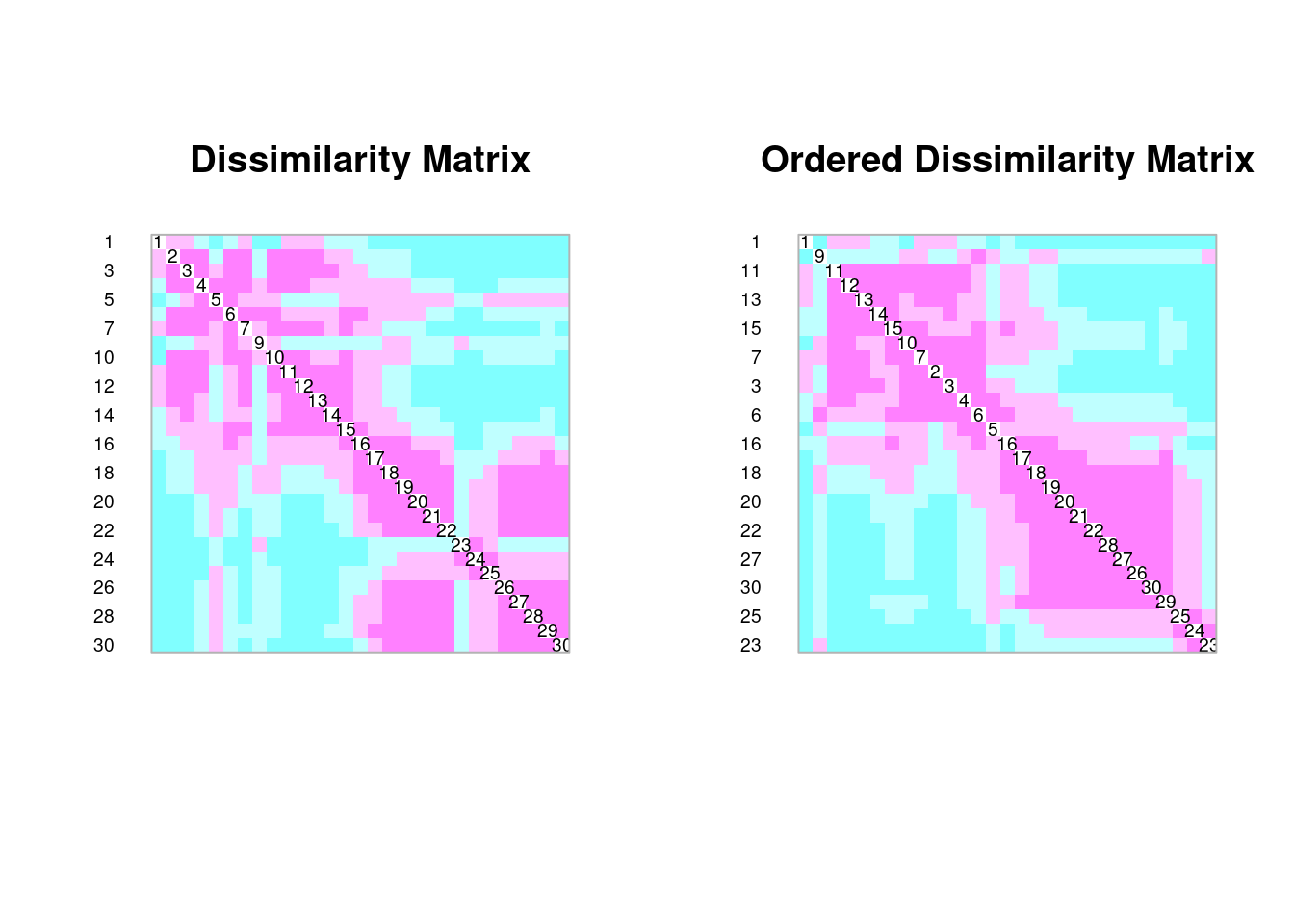
Comparando comunidades com dados binários (Q-mode)
Há muitas ocasiões em que temos apenas dados de presença ou ausência das espécies que estudamos. Isso é muito comum para grupos biológicos onde as abundâncias não podem ser medidas com precisão, como briófitas ou grandes mamíferos. Os dados de presença e ausência também podem ser “gerados”, covnertendo à partir das abundâncias. Há perguntas especpíficas e áreas de conhecimento como a Biogeografia, onde a presença/ausência pode ser mais informativa que as abundâncias. Esses dados são geralmente tratados com índices em vez de medidas distância porque justamente, eles não cumprem com os pré-requisitos para serem considerados simétricos.
 fig by
David Zelený
fig by
David Zelený
Prós e contras de dados de abundância e presença e ausência
- Dados de abundância podem se transformados em presença/ausência. Não o contrário
- Abundâncias são informações valiosas para muuuuitas análises ecológicas. Sempre procure coletar abundâncias.
- Abundância traz pelos menos duas informações ecológicas importantes:
- A óbvia ocorrência ou não de uma espécie num determinado gradiente ambiental, e;
- O grau de adaptabilidade (fitness) que essa espécie possui. Quanto mais abundante, melhor o habitat para ela, em tese.
- A abundância também informa sobre as interações bióticas, que provavelmente favorecem espécies abundantes.
- A ocorrência é mito poderosa para testar limitação de dispesão de espécies, ou seja, a probabilidade de encontrar espécies ao longo de uma paisagem ou gradiente ambiental.
- As ocorrências são poderosas para testar relações com gradientes ambientais em análises do tipo “unconstrained”, que não vamos abordar muito nessa disciplina mas que eventualmente podemos precisar.
Exemplos da literatura

Neste trabalho de Lobo et al (2011) mostramos como a Mata Atlântica vem sofrendo com o processod e homogeneização biótica decorrente da perturbação antrópica. Testamos isso justamente com uma matriz de similaridade de espécies qque agrupamos em 12 tipos de fitofisionomias e em dois períodos de tempo (prá-1980 e pós-1980). Nossos dados eram apenas de presença e ausência em localidades de coleta, através de dados de herbário. Dê uma olhada no artigo e veja como dados de ocorrência foram usados.
 Neste artigo
Scholar et al (2016) mostram como o domínio conceitua da beta-diversidade é importante para pensar e planejar a conservação da biodiversidade. Aqui não te nada de índices nem medidas mas conceitos. Esses conceitos dão sentido às perguntas que fazemos na ciência e ajudam a escolher as melhores métricas.
Neste artigo
Scholar et al (2016) mostram como o domínio conceitua da beta-diversidade é importante para pensar e planejar a conservação da biodiversidade. Aqui não te nada de índices nem medidas mas conceitos. Esses conceitos dão sentido às perguntas que fazemos na ciência e ajudam a escolher as melhores métricas.
Os desdrobamentos dos conceitos e aplicações da beta-diversidade são fundamentais para uma correta aplicação das métricas de assossiação. Índices de similaridade e medidas de distância são maneiras de quantificar diversidade beta entre comunidades biológicas.
Q mode para dados ambientais
As vairáveis ambientais env são dados contínuos que não possuem “problema” dos duplos zeros. Potanto, as medidas de distância são perfeitamente aplicáveis a elas. Dessas, a distância euclidiana, que á a distãncia entre dois pontos medida pela clássica fórmula de Pitágoras, é a medida de escolha inicial.
env2<- env[,-1] # remover 'dfs' que é uma variável espacial, não ambiental
env.de<-dist(scale(env2)) # use a função "scale" para transformar osdados em z-scores, já que dados de magnitude muito diferentes podem criar disorções no cálculo de distâncias.
corrplot(as.matrix(env.de), is.corr = FALSE)
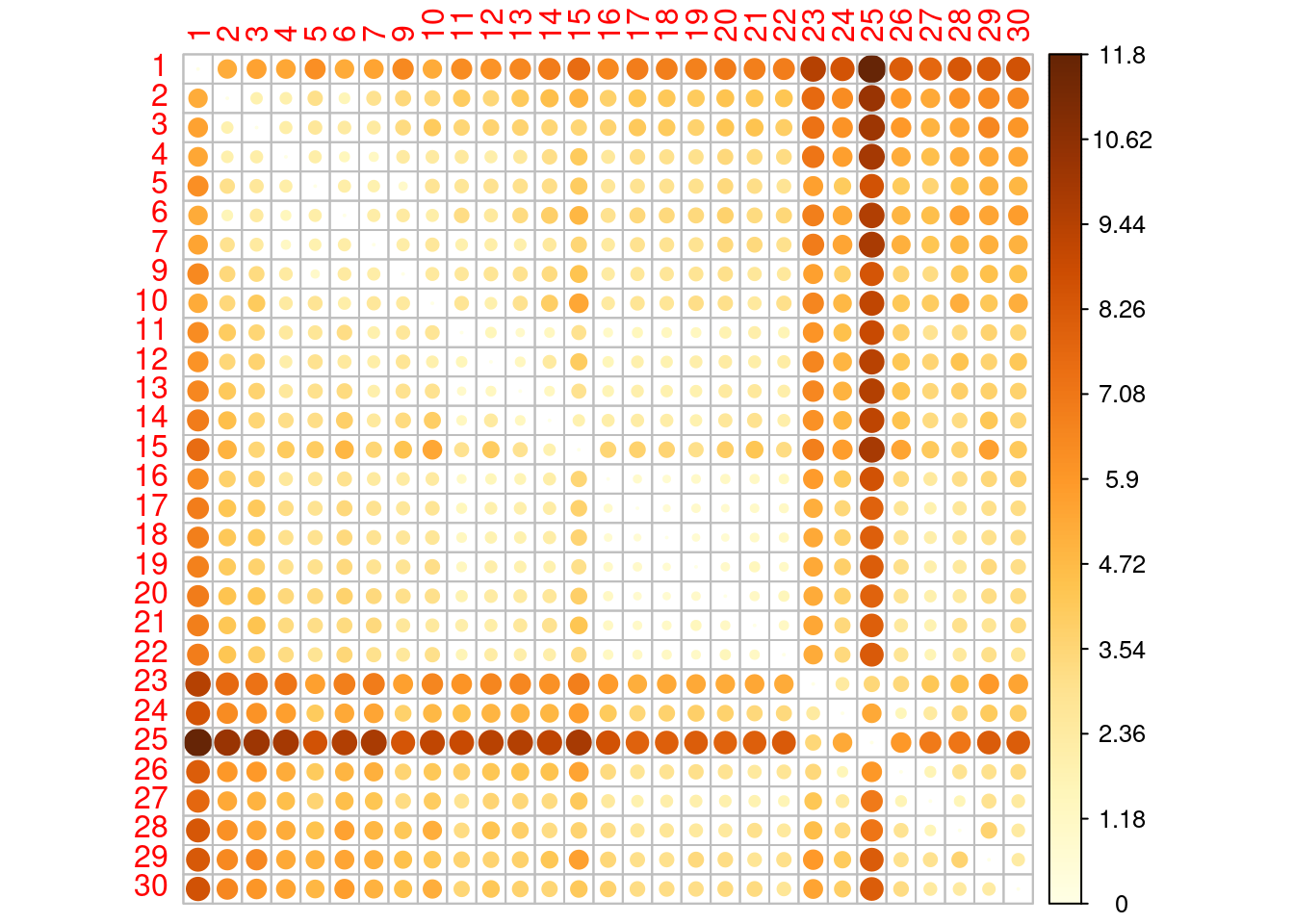
Lembrem-se que nessa matriz, os números são as amostras, que começam em 1 na nascente do rio e terminam em 30 no ponto mais distante. Conseguem ver algum padrão? tentem entender a matriz, dê exemplos de pontos muitos parecidos e outros muito dissimilares. Será que você está lendo a matriz corretamente?
Distâncias geográficas
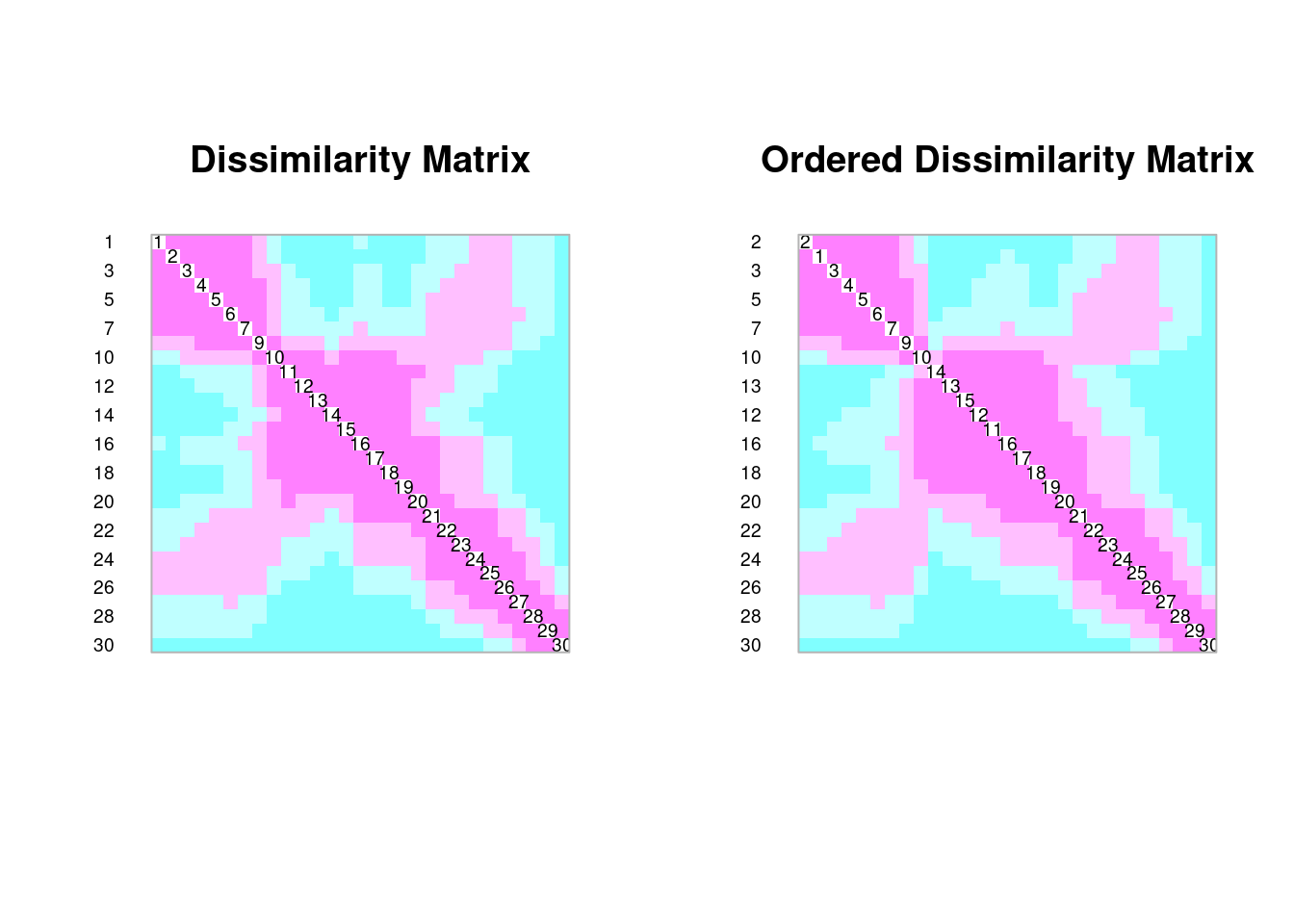
spa.de<-dist(spa)
coldiss(spa.de, diag = TRUE)
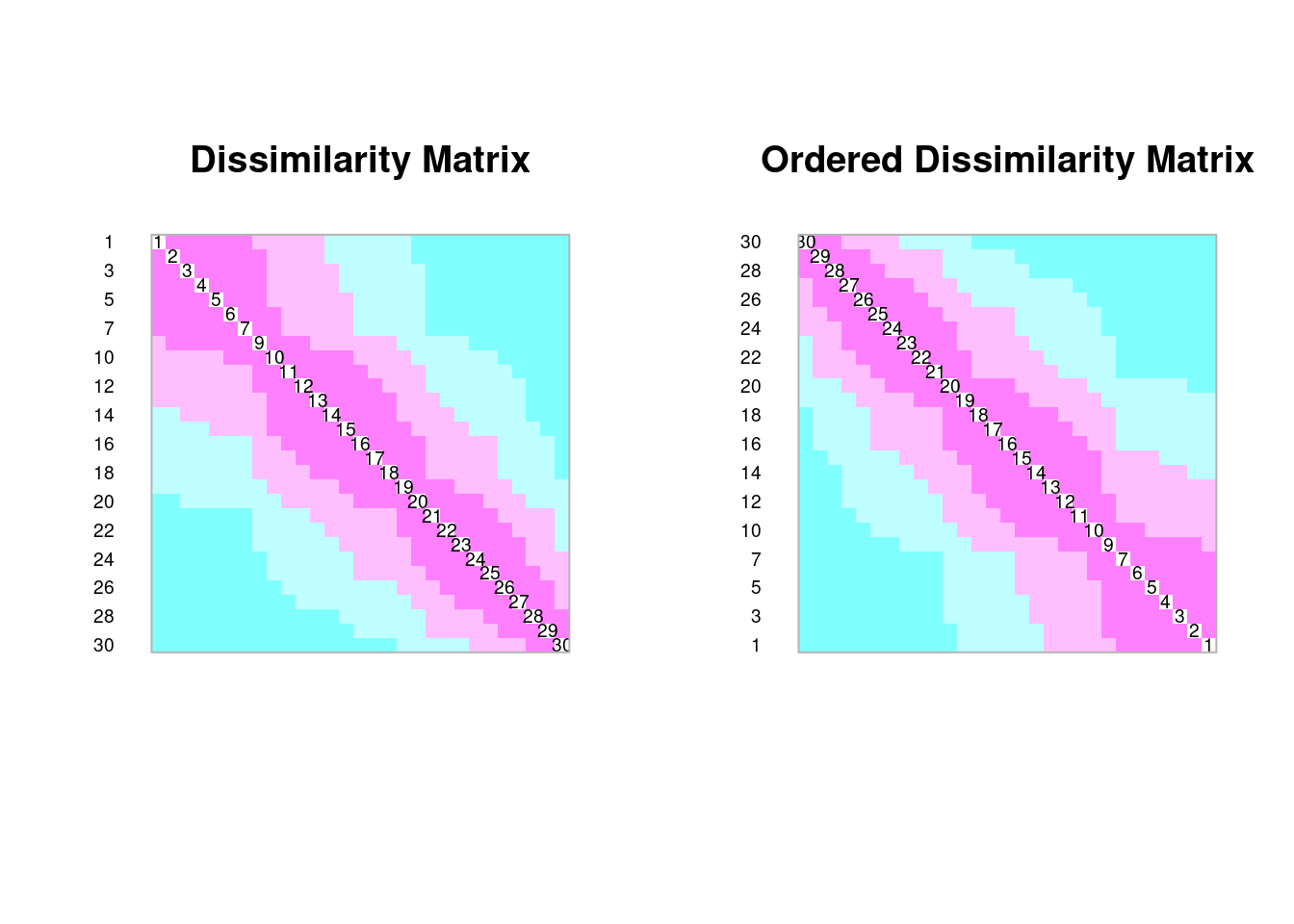
dfs.df<-as.data.frame(env$dfs, row.names = rownames(env))
riv.de<-dist(dfs.df)
coldiss(riv.de, diag = TRUE)
R mode para dados ambientais ou espécies
A lógica aqui é saber quais variáveis ou espécies estão correlacionadas e não o quão similar cada par de site ou espécies pode ser. Nesse caso, usamos basicamente testes de correlação ou covariança. Essa informação é poderosa, pois pode tanto expressar gradientes ambientais complexos (várias variáveis ambientais se comportnaod de maneira similar) ou a co-ocorrência de espécies. Vejamos:
Variáveis ambientais
cor.env<-cor(env2)
coldiss(cor.env, diag = T)
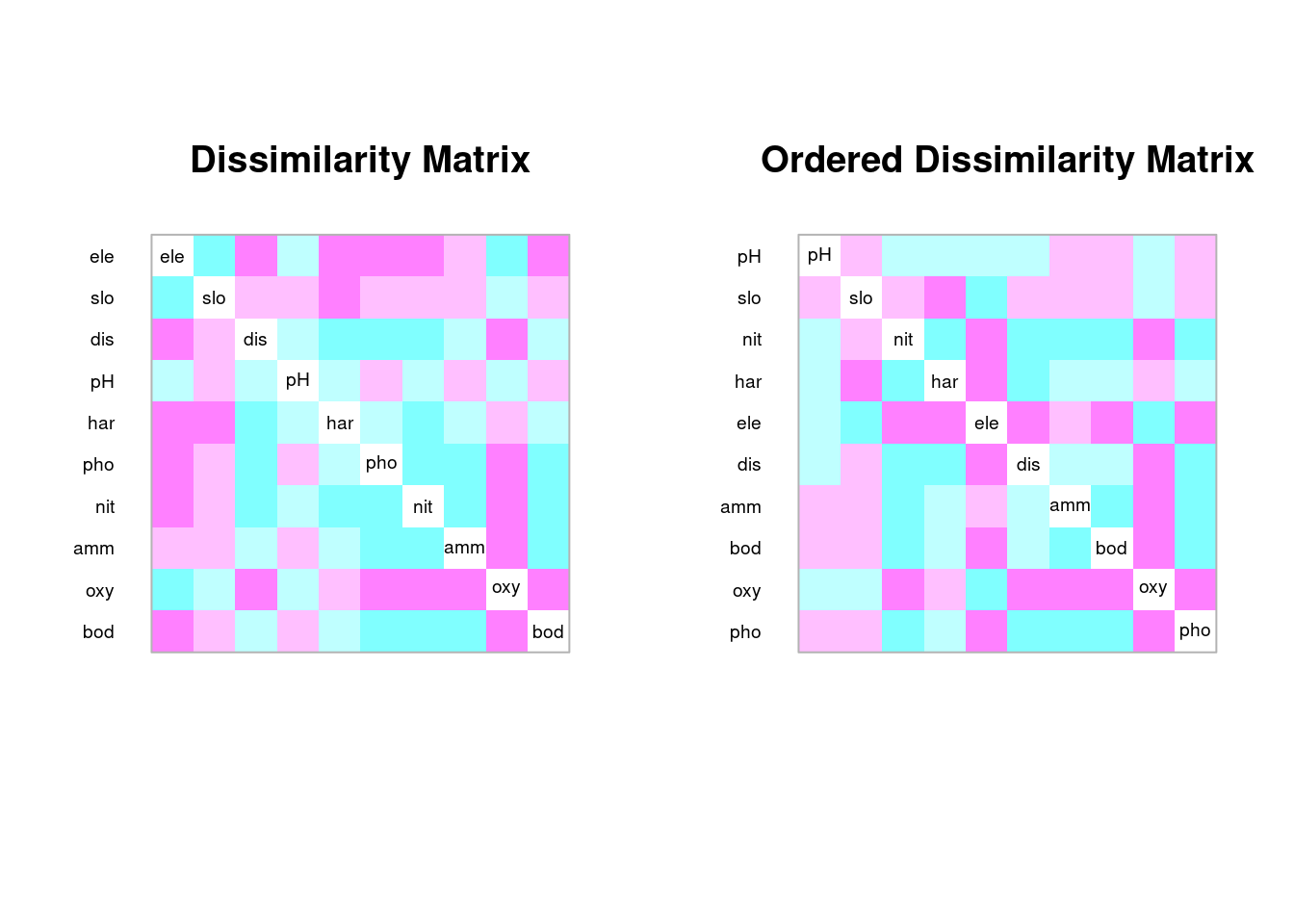
Consegue ideintificar grupos de variáveis ambientais que covariam?
Espécies que covariam
spe.t <- t(spe)
# Chi-square pre-transformation followed by Euclidean distance
spe.t.chi <- decostand(spe.t, "chi.square")
spe.t.D16 <- dist(spe.t.chi)
coldiss(spe.t.D16, diag = TRUE)
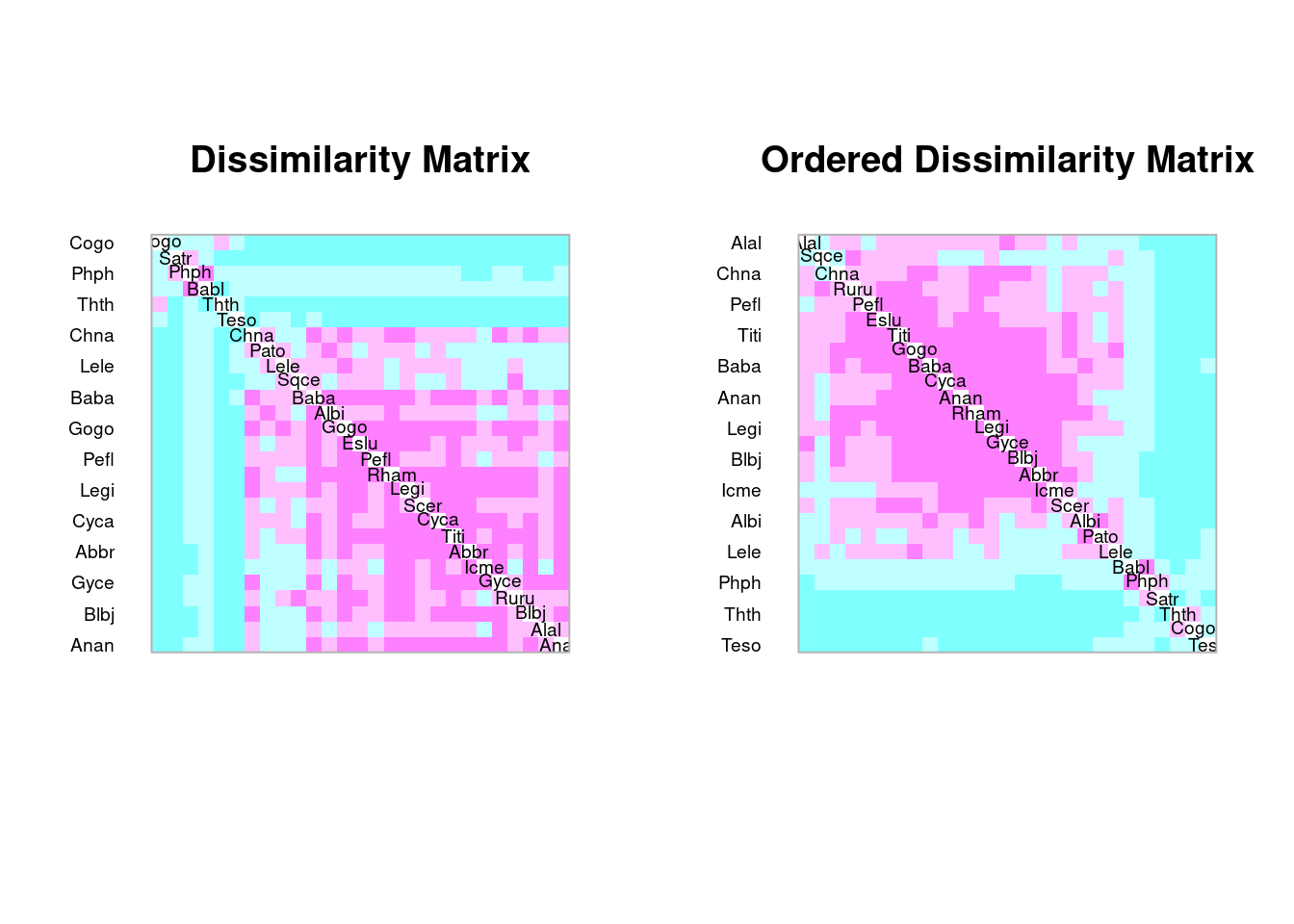
Consegue identificar grupos de espécies?
Em resumo…

Exemplos sobre Medidas de associação
As bases de dados do livro Numerical Ecology estão compostas por três matrizes, uma de espécies “spe”, outra de variáveis ambientais “env” e outra de variáveis geográficas “spa”. Agora que sabemos que as medidas de associação servem para medir a similaridade entre “objetos” que podem ser de qualquer natureza, vamos fazer alguns exerícios.
Aqui vou demonstrar através de uma pergunta simples, como explorar as medidas de similaridade de modo a obter das bases de dados ecológicos algumas informações importantes para compreender a estrutura de comunidades biológicas e os processos que às mantêm.
Nesse caso, vou dividir o rio em três seções: “alto”, “médio” e “baixo”. As amostras de 1 a 10 serão o “alto rio”; as de 11-20 serão o “médio rio” e as de 21-30 serão o “baixo rio”. Para isso, vou acrescentar uma coluna com essa informação à bases de dados
Pergunta 1 - Qual a similaridade entre as comunidades de peixes do alto, médio e baixo curso de rio?
método 1) Usando índices de similaridade
jacc_dist<-vegdist(spe[,-28], method = "jaccard") # retirei somente a coluna "rio" porque a função só lê variáveis numéricas
jacc_dist # Dê uma olhada na matriz, note que os valores estão entre 0 e 1 como previsto
## 1 2 3 4 5 6 7
## 2 0.7500000
## 3 0.8125000 0.2500000
## 4 0.8571429 0.5000000 0.3181818
## 5 0.9428571 0.8205128 0.8095238 0.6585366
## 6 0.8571429 0.5652174 0.4583333 0.3200000 0.5897436
## 7 0.8125000 0.2500000 0.2222222 0.3913043 0.7804878 0.3913043
## 9 1.0000000 0.8181818 0.8461538 0.7931034 0.7368421 0.7037037 0.8000000
## 10 0.9375000 0.5555556 0.5714286 0.5416667 0.7027027 0.4090909 0.4210526
## 11 0.7272727 0.4666667 0.5789474 0.6086957 0.8157895 0.6086957 0.5000000
## 12 0.8333333 0.3333333 0.3809524 0.5000000 0.8181818 0.5555556 0.3000000
## 13 0.8421053 0.4500000 0.4782609 0.6206897 0.8478261 0.7096774 0.5416667
## 14 0.8928571 0.5714286 0.4827586 0.5151515 0.8076923 0.6000000 0.5333333
## 15 0.9090909 0.6764706 0.6388889 0.5789474 0.7115385 0.5405405 0.5588235
## 16 0.9250000 0.7906977 0.7272727 0.6444444 0.6296296 0.5476190 0.6976744
## 17 0.9555556 0.8085106 0.7755102 0.6734694 0.6779661 0.6170213 0.7500000
## 18 0.9772727 0.8510638 0.8400000 0.7400000 0.6666667 0.6875000 0.8163265
## 19 1.0000000 0.8846154 0.8301887 0.7592593 0.6666667 0.6862745 0.8076923
## 20 1.0000000 0.9538462 0.9411765 0.8507463 0.6567164 0.8153846 0.9253731
## 21 1.0000000 0.9722222 0.9600000 0.8783784 0.6666667 0.8472222 0.9459459
## 22 1.0000000 0.9879518 0.9767442 0.9058824 0.6913580 0.8795181 0.9647059
## 23 1.0000000 1.0000000 1.0000000 0.9583333 0.9444444 0.9130435 0.9473684
## 24 1.0000000 1.0000000 1.0000000 0.9411765 0.8863636 0.8750000 0.9666667
## 25 1.0000000 1.0000000 0.9615385 0.8965517 0.8157895 0.8148148 0.9200000
## 26 1.0000000 0.9814815 0.9649123 0.8771930 0.7166667 0.8148148 0.9464286
## 27 1.0000000 0.9864865 0.9740260 0.9090909 0.7236842 0.8648649 0.9605263
## 28 1.0000000 0.9876543 0.9761905 0.9036145 0.7317073 0.8765432 0.9638554
## 29 0.9887640 0.9687500 0.9595960 0.8979592 0.6989247 0.8750000 0.9489796
## 30 1.0000000 1.0000000 0.9903846 0.9320388 0.7448980 0.9108911 0.9805825
## 9 10 11 12 13 14 15
## 2
## 3
## 4
## 5
## 6
## 7
## 9
## 10 0.7272727
## 11 0.8636364 0.6111111
## 12 0.8148148 0.5454545 0.3888889
## 13 0.9000000 0.7307692 0.5000000 0.3181818
## 14 0.8648649 0.6451613 0.6071429 0.3571429 0.3214286
## 15 0.7948718 0.5757576 0.6666667 0.5000000 0.5555556 0.3947368
## 16 0.8260870 0.6829268 0.7857143 0.7111111 0.7446809 0.6122449 0.4130435
## 17 0.8163265 0.6818182 0.7777778 0.7346939 0.7647059 0.6666667 0.5740741
## 18 0.7826087 0.7272727 0.8222222 0.8000000 0.8269231 0.7500000 0.6363636
## 19 0.8000000 0.7755102 0.9038462 0.8571429 0.8983051 0.8064516 0.7258065
## 20 0.8135593 0.8709677 0.9531250 0.9428571 0.9583333 0.9090909 0.8289474
## 21 0.8656716 0.8985507 0.9571429 0.9610390 0.9746835 0.9285714 0.8690476
## 22 0.8684211 0.9250000 0.9753086 0.9772727 0.9888889 0.9473684 0.8709677
## 23 0.8750000 0.9411765 0.9285714 0.9523810 1.0000000 0.9677419 0.9722222
## 24 0.8400000 0.8846154 0.9600000 0.9687500 1.0000000 0.9512195 0.9333333
## 25 0.9130435 0.8636364 0.9523810 0.9642857 1.0000000 0.9166667 0.9000000
## 26 0.8367347 0.9038462 0.9615385 0.9661017 0.9836066 0.9242424 0.8656716
## 27 0.8676471 0.9154930 0.9722222 0.9746835 0.9876543 0.9418605 0.8705882
## 28 0.8648649 0.9230769 0.9746835 0.9767442 0.9886364 0.9462366 0.8804348
## 29 0.8777778 0.9139785 0.9462366 0.9500000 0.9504950 0.9150943 0.8461538
## 30 0.9157895 0.9489796 0.9898990 0.9905660 1.0000000 0.9646018 0.9009009
## 16 17 18 19 20 21 22
## 2
## 3
## 4
## 5
## 6
## 7
## 9
## 10
## 11
## 12
## 13
## 14
## 15
## 16
## 17 0.4150943
## 18 0.5090909 0.2448980
## 19 0.5666667 0.4745763 0.4000000
## 20 0.7368421 0.5915493 0.4923077 0.3809524
## 21 0.7710843 0.6582278 0.5753425 0.4571429 0.1846154
## 22 0.7956989 0.7111111 0.6428571 0.5609756 0.3157895 0.1891892
## 23 0.9523810 0.9090909 0.9047619 0.9130435 0.9285714 0.9354839 0.9444444
## 24 0.9000000 0.8200000 0.7872340 0.7800000 0.7321429 0.7580645 0.7916667
## 25 0.8666667 0.8541667 0.7954545 0.7608696 0.8035714 0.8225806 0.8472222
## 26 0.7794118 0.7014925 0.6290323 0.4915254 0.3500000 0.3333333 0.4027778
## 27 0.8023256 0.7261905 0.6538462 0.5466667 0.3239437 0.2394366 0.2236842
## 28 0.8172043 0.7333333 0.6666667 0.5853659 0.3636364 0.2857143 0.2250000
## 29 0.7904762 0.6767677 0.6129032 0.5851064 0.3932584 0.3068182 0.2134831
## 30 0.8378378 0.7333333 0.6900000 0.6500000 0.4574468 0.3763441 0.3052632
## 23 24 25 26 27 28 29
## 2
## 3
## 4
## 5
## 6
## 7
## 9
## 10
## 11
## 12
## 13
## 14
## 15
## 16
## 17
## 18
## 19
## 20
## 21
## 22
## 23
## 24 0.7333333
## 25 0.6363636 0.6315789
## 26 0.9069767 0.6511628 0.7441860
## 27 0.9365079 0.7619048 0.8253968 0.3174603
## 28 0.9428571 0.7857143 0.8428571 0.3857143 0.1780822
## 29 0.9540230 0.8275862 0.8735632 0.5057471 0.3146067 0.2555556
## 30 0.9550562 0.8314607 0.8764045 0.5333333 0.3296703 0.2717391 0.2574257
Bom, uma maatriz desse tamanho e con tantas cálulas é difícil de usar para responder a nossa pergunta… mas podemos dar um jeito nisso.
mean(jacc_dist) # Esse é o valor médio da similaridade de jaccard entre todas as combinações possíveis
## [1] 0.7540221
library(usedist)
mean(dist_subset(jacc_dist, c(1:8))) # vai pegar as primeiras 9 linhas da matriz e calcular a similaridade média. Isso equivale a similaridade de alto rio
## [1] 0.6448391
mean(dist_subset(jacc_dist, c(9:18))) # Agora para o médio rio
## [1] 0.6223917
mean(dist_subset(jacc_dist, c(19:28))) # Agora para o baixo rio
## [1] 0.5761246
Alguma diferença? Dá pra ver assim no olhômetro?
Talvez a melhor maneira de visualizar esses pontos seja fazendo um dendograma
clust_rio<-hclust(jacc_dist, method = "complete")
clust_graf<-plot(clust_rio, hang=-1)
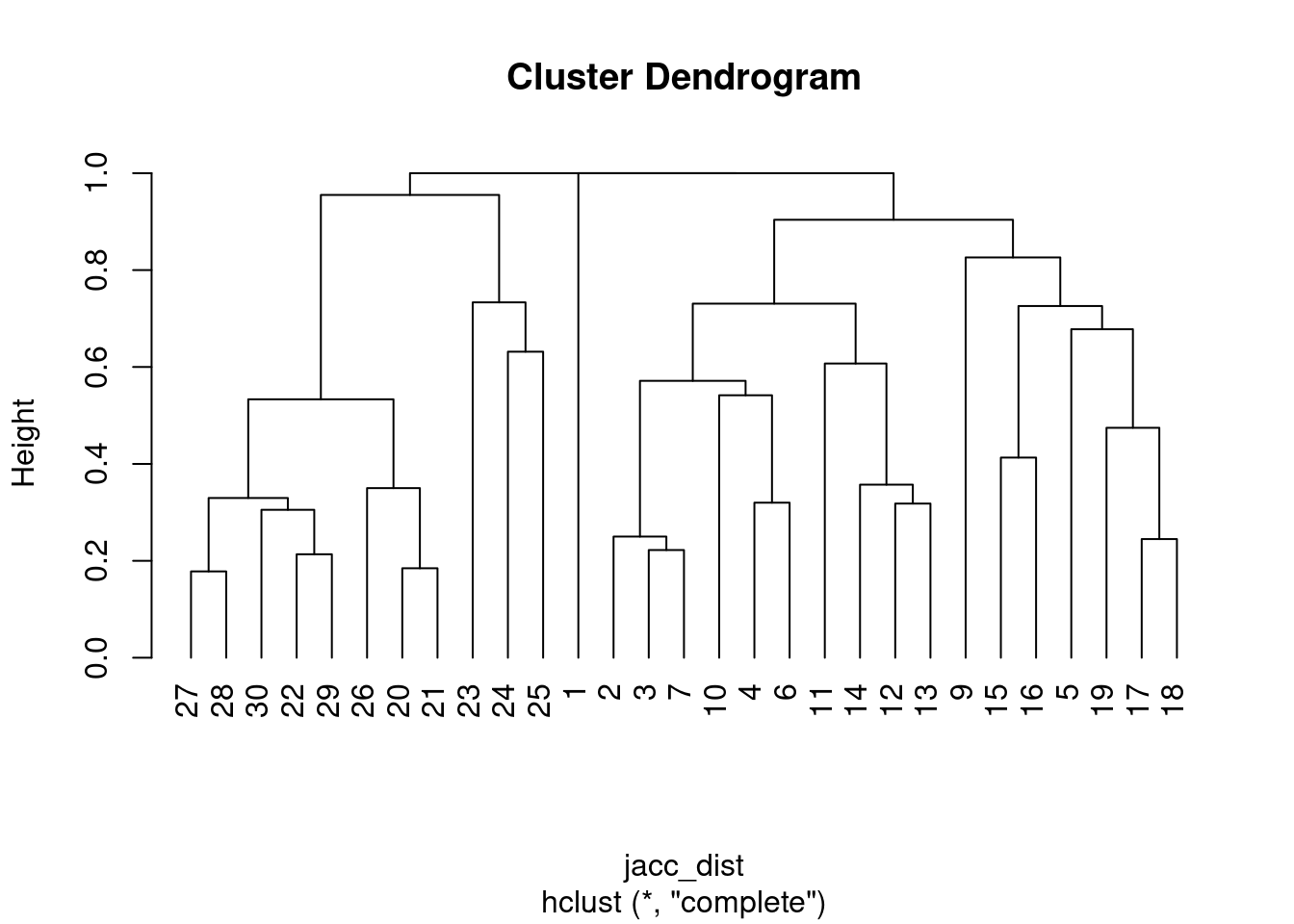
clust_graf
## NULL
Mas não cosigo ver se os grupos que atribui de alto, médio e baixo rio, realmente agrupam as espécies. Vamos fazer algumas modificações nas bases para poder ver se nossa ideia faz sentido, ou seja, se as espécies se agrupam entre alto, médio e baixo rio.
Agora podemos plotar o dendograma onde: números amarelos são do alto rio, azuis do médio rio e verdes do baixo rio.
plot(clust_rio2)
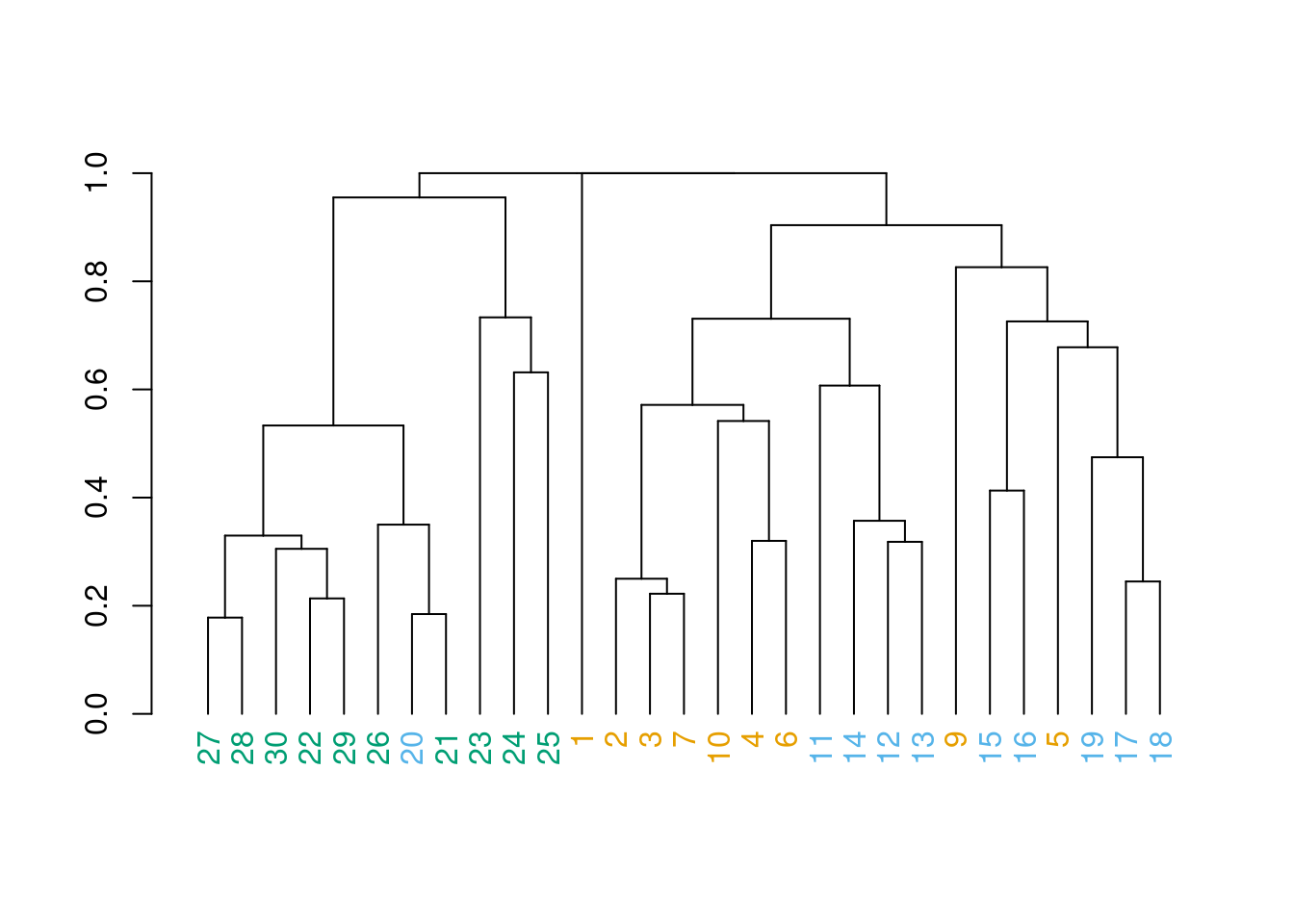
Temos padrão?
E se usássemos em vez do índice de Jaccard, a distância euclidiana? Será que teríamos mais sensibilidade para identificar esses agrupamentos que imaginamos que existem?
euc_dist<-vegdist(spe[,-28], method = "euclidean") # agora é com a distância euclideana
euc_dist
## 1 2 3 4 5 6 7
## 2 5.385165
## 3 7.416198 2.449490
## 4 7.874008 4.123106 3.000000
## 5 10.816654 10.677078 10.862780 9.219544
## 6 7.348469 4.582576 4.123106 2.828427 8.185353
## 7 6.855655 2.449490 2.000000 3.605551 10.488088 3.605551
## 9 7.810250 8.717798 9.380832 8.774964 9.380832 6.708204 8.485281
## 10 6.708204 5.099020 5.291503 5.000000 9.273618 3.605551 4.472136
## 11 4.472136 3.316625 5.000000 5.477226 10.246951 5.291503 4.795832
## 12 6.708204 3.162278 3.464102 4.582576 11.045361 4.795832 3.162278
## 13 7.071068 4.358899 5.196152 6.164414 11.532563 6.633250 5.385165
## 14 9.110434 6.324555 6.164414 6.557439 11.916375 7.000000 6.324555
## 15 9.899495 7.810250 7.681146 7.483315 10.816654 6.633250 6.855655
## 16 11.090537 9.899495 9.797959 9.327379 10.198039 8.426150 9.055385
## 17 10.630146 9.486833 9.486833 8.774964 9.797959 8.062258 9.055385
## 18 9.848858 9.591663 9.899495 8.660254 9.055385 7.810250 9.380832
## 19 11.704700 11.135529 11.045361 10.148892 9.380832 8.888194 10.770330
## 20 13.453624 14.212670 14.628739 13.453624 10.770330 12.206556 14.212670
## 21 14.456832 15.362291 15.811388 14.525839 11.489125 13.601471 15.556349
## 22 16.643317 17.663522 18.110770 16.763055 13.416408 15.779734 17.663522
## 23 3.872983 7.483315 9.055385 9.000000 10.583005 7.937254 8.485281
## 24 7.071068 9.539392 10.816654 10.583005 11.357817 9.486833 10.246951
## 25 5.291503 8.306624 9.643651 9.273618 9.746794 8.246211 9.110434
## 26 11.135529 12.609520 13.304135 12.409674 10.723805 11.224972 12.922848
## 27 15.362291 16.462078 16.881943 15.811388 13.076697 14.696938 16.583124
## 28 16.522712 17.549929 18.000000 16.941074 14.352700 15.905974 17.606817
## 29 18.761663 19.364917 19.621417 18.384776 15.524175 17.776389 19.364917
## 30 20.396078 21.377558 21.794495 20.542639 17.117243 19.849433 21.517435
## 9 10 11 12 13 14 15
## 2
## 3
## 4
## 5
## 6
## 7
## 9
## 10 6.480741
## 11 7.549834 4.582576
## 12 8.717798 5.477226 3.872983
## 13 10.049876 6.855655 4.000000 3.316625
## 14 10.583005 7.615773 6.244998 4.242641 3.316625
## 15 9.746794 6.855655 7.745967 6.403124 6.633250 5.000000
## 16 10.862780 8.485281 10.049876 9.591663 9.746794 8.944272 5.916080
## 17 9.899495 8.246211 9.219544 9.273618 9.643651 9.380832 8.185353
## 18 8.602325 7.874008 8.774964 9.380832 9.949874 9.797959 8.660254
## 19 9.486833 9.273618 11.000000 11.313708 12.041595 11.832160 10.630146
## 20 11.489125 12.727922 13.527749 14.422205 15.000000 14.966630 13.674794
## 21 13.266499 14.142136 14.662878 15.684387 16.031220 16.062378 15.066519
## 22 15.033296 16.248077 16.941074 17.832555 18.303005 18.165902 16.763055
## 23 6.324555 6.633250 5.744563 8.366600 8.774964 10.392305 10.630146
## 24 7.549834 8.544004 8.124038 10.148892 10.583005 11.789826 11.747340
## 25 7.280110 7.000000 6.782330 9.110434 9.486833 10.723805 10.583005
## 26 10.148892 11.445523 11.747340 13.000000 13.490738 13.892444 13.190906
## 27 13.892444 15.264338 15.748016 16.703293 17.146428 17.117243 16.062378
## 28 14.899664 16.309506 16.822604 17.720045 18.193405 18.220867 17.175564
## 29 17.521415 18.303005 18.761663 19.416488 19.646883 19.313208 18.330303
## 30 19.467922 20.371549 20.736441 21.610183 21.863211 21.931712 21.023796
## 16 17 18 19 20 21 22
## 2
## 3
## 4
## 5
## 6
## 7
## 9
## 10
## 11
## 12
## 13
## 14
## 15
## 16
## 17 6.164414
## 18 7.615773 3.464102
## 19 9.165151 6.633250 6.000000
## 20 12.649111 9.380832 7.615773 6.324555
## 21 13.928388 11.224972 9.380832 7.874008 3.741657
## 22 15.556349 13.416408 11.489125 10.583005 6.480741 4.000000
## 23 11.489125 10.295630 9.055385 10.488088 11.916375 13.114877 15.362291
## 24 12.449900 10.723805 9.110434 9.746794 10.148892 11.269428 13.304135
## 25 11.180340 10.148892 8.660254 9.539392 10.630146 11.618950 13.964240
## 26 13.076697 10.816654 8.774964 7.810250 5.385165 5.385165 7.549834
## 27 15.329710 13.304135 11.532563 10.246951 6.244998 4.582576 5.000000
## 28 16.370706 14.352700 12.489996 11.489125 7.745967 6.000000 5.099020
## 29 17.058722 14.662878 13.076697 12.767145 9.000000 7.000000 5.567764
## 30 19.621417 17.117243 15.652476 15.000000 11.180340 9.000000 8.185353
## 23 24 25 26 27 28 29
## 2
## 3
## 4
## 5
## 6
## 7
## 9
## 10
## 11
## 12
## 13
## 14
## 15
## 16
## 17
## 18
## 19
## 20
## 21
## 22
## 23
## 24 4.358899
## 25 3.000000 3.741657
## 26 9.433981 7.071068 8.000000
## 27 14.035669 11.916375 12.649111 5.291503
## 28 15.231546 13.076697 13.964240 7.000000 3.872983
## 29 17.804494 15.874508 16.431677 9.899495 6.633250 5.567764
## 30 19.416488 17.832555 18.055470 11.916375 9.165151 7.280110 6.480741
Vamos ver como ficam os índices…
mean(euc_dist) # Esse é o valor médio da similaridade de jaccard entre todas as combinações possíveis
## [1] 10.82614
library(usedist)
mean(dist_subset(euc_dist, c(1:8))) # vai pegar as primeiras 9 linhas da matriz e calcular a similaridade média. Isso equivale a similaridade de alto rio
## [1] 6.684087
mean(dist_subset(euc_dist, c(9:18))) # Agora para o médio rio
## [1] 7.742624
mean(dist_subset(euc_dist, c(19:28))) # Agora para o baixo rio
## [1] 8.99927
E agora, compare os resultados com aqueles do índice de Jaccard, alguma coisa mudou?
clust_rio_euc<-hclust(euc_dist, method = "complete")
clust_graf_euc<-plot(clust_rio_euc, hang=-1)
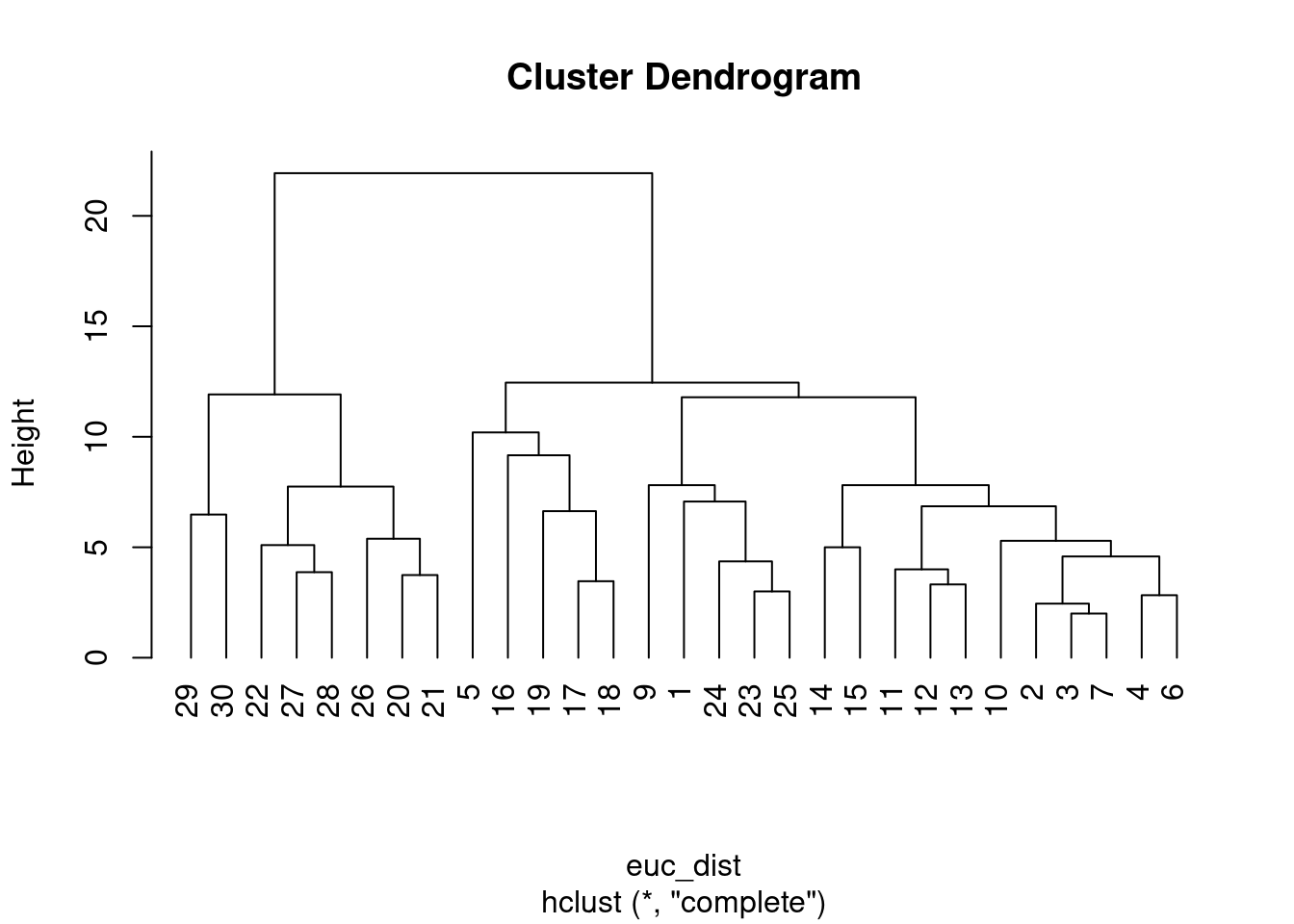
clust_graf_euc
## NULL
Agora vamos colorir o dendograma
clust_rio_euc2<-as.dendrogram(clust_rio_euc) # trandformando o cluster num objeto para poder editar
colors<-c("#E69F00","#56B4E9", "#009E73") # definindo as cores que serão usadas
colorCode<-c(alto=colors[1], medio=colors[2], baixo=colors[3])
labels_colors(clust_rio_euc2) <- colorCode[rio][order.dendrogram(clust_rio_euc2)]
Agora podemos plotar o dendograma onde: números amarelos são do alto rio, azuis do médio rio e pretos do baixo rio.
plot(clust_rio_euc2)
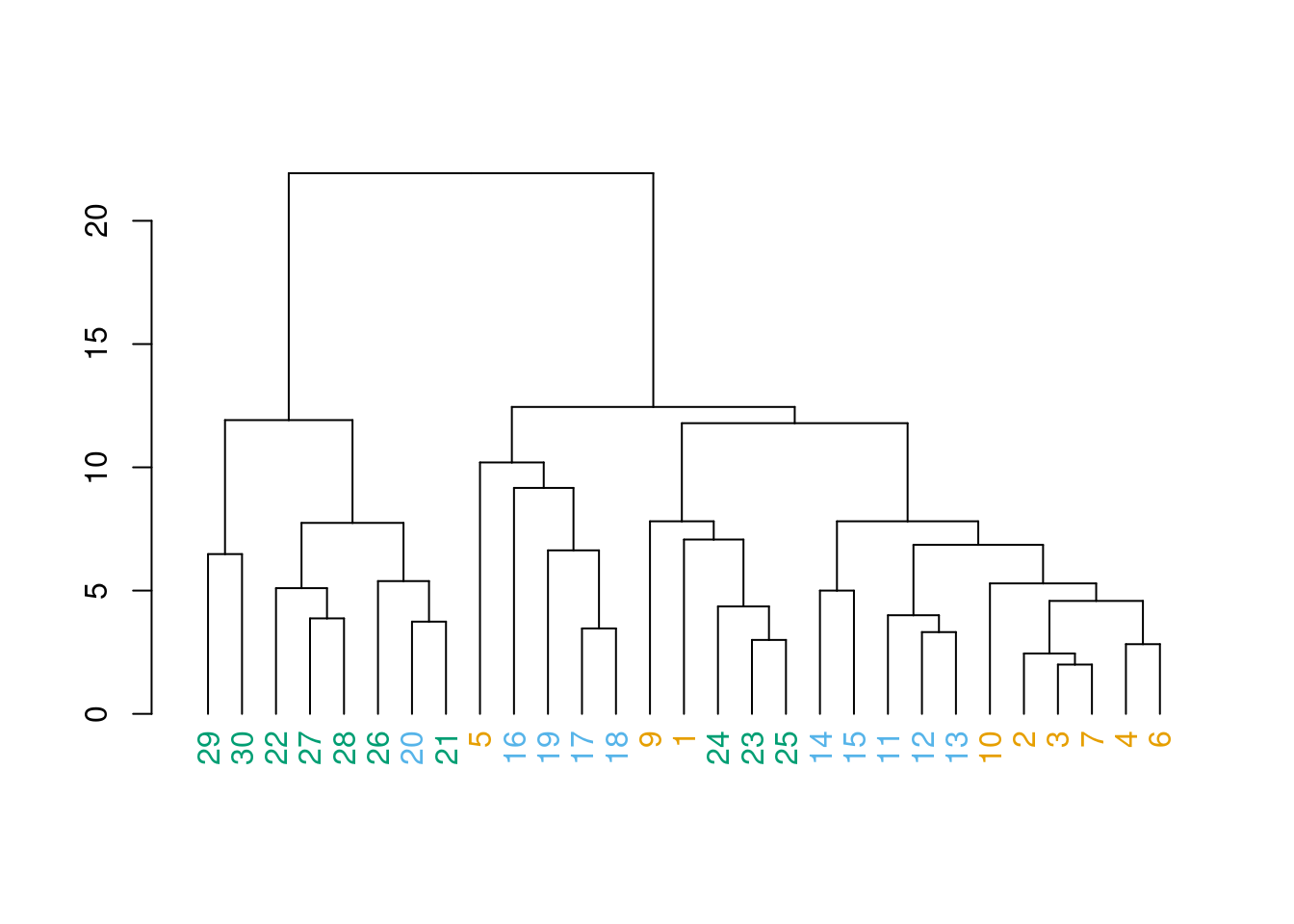
Novamente, temos alguma diferença que aponta para uma certa organização das espécies, mas notem que agora parecem mais misturados que quando usamos o índice de Jaccard, mas mesmo essa “mistura” tem um certo padrão, podem perceber?
Aparentemente o médio rio é uma interseção entre comunidades de baixo e alto rio. Será que as variáveis ambientais conseguem explicar isso?
Vamos aplicar o mesmo passo-à-passo para a matriz ambiental
env[,-c(1,4,12)] # aqui eu retirei duas colunas, a que adicionamos com o trecho do rio a quarta e a primeira que eraa distancia linear entre a primeira e as demais amostras.
## ele slo pH har pho nit amm oxy bod
## 1 934 48.0 7.9 45 0.01 0.20 0.00 12.2 2.7
## 2 932 3.0 8.0 40 0.02 0.20 0.10 10.3 1.9
## 3 914 3.7 8.3 52 0.05 0.22 0.05 10.5 3.5
## 4 854 3.2 8.0 72 0.10 0.21 0.00 11.0 1.3
## 5 849 2.3 8.1 84 0.38 0.52 0.20 8.0 6.2
## 6 846 3.2 7.9 60 0.20 0.15 0.00 10.2 5.3
## 7 841 6.6 8.1 88 0.07 0.15 0.00 11.1 2.2
## 9 752 1.2 8.0 90 0.30 0.82 0.12 7.2 5.2
## 10 617 9.9 7.7 82 0.06 0.75 0.01 10.0 4.3
## 11 483 4.1 8.1 96 0.30 1.60 0.00 11.5 2.7
## 12 477 1.6 7.9 86 0.04 0.50 0.00 12.2 3.0
## 13 450 2.1 8.1 98 0.06 0.52 0.00 12.4 2.4
## 14 434 1.2 8.3 98 0.27 1.23 0.00 12.3 3.8
## 15 415 0.5 8.6 86 0.40 1.00 0.00 11.7 2.1
## 16 375 2.0 8.0 88 0.20 2.00 0.05 10.3 2.7
## 17 349 0.5 8.0 92 0.20 2.50 0.20 10.2 4.6
## 18 333 0.8 8.0 90 0.50 2.20 0.20 10.3 2.8
## 19 310 0.5 8.1 84 0.60 2.20 0.15 10.6 3.3
## 20 286 0.8 8.0 86 0.30 3.00 0.30 10.3 2.8
## 21 262 1.0 7.9 85 0.20 2.20 0.10 9.0 4.1
## 22 254 1.4 8.1 88 0.20 1.62 0.07 9.1 4.8
## 23 246 1.2 8.1 97 2.60 3.50 1.15 6.3 16.4
## 24 241 0.3 8.0 99 1.40 2.50 0.60 5.2 12.3
## 25 231 0.5 7.9 100 4.22 6.20 1.80 4.1 16.7
## 26 214 0.5 7.9 94 1.43 3.00 0.30 6.2 8.9
## 27 206 1.2 8.1 90 0.58 3.00 0.26 7.2 6.3
## 28 195 0.3 8.3 100 0.74 4.00 0.30 8.1 4.5
## 29 183 0.6 7.8 110 0.45 1.62 0.10 9.0 4.2
## 30 172 0.2 8.2 109 0.65 1.60 0.10 8.2 4.4
env_dist<-vegdist(env[,-c(1,4,12)], method = "euclidean")
env_dist
## 1 2 3 4 5 6 7
## 2 45.368162
## 3 49.144527 21.706769
## 4 95.600514 84.314332 63.288507
## 5 104.233868 94.071898 72.558676 14.249368
## 6 99.934171 88.360992 68.496496 14.988782 24.325076
## 7 110.514552 102.950061 81.458626 20.913979 11.152264 28.827711
## 9 193.315760 186.880184 166.458846 103.740428 97.200632 98.739522 89.324667
## 10 321.430171 317.872399 298.578252 237.327355 232.150213 230.155056 224.118340
## 11 455.995377 452.484639 433.244515 371.782197 366.236198 364.796399 358.101683
## 12 461.175824 457.326897 438.329546 377.269118 372.043769 369.931072 364.042598
## 13 489.052231 485.482846 466.282653 404.841312 399.288094 397.837475 391.156129
## 14 504.976978 501.378174 482.210173 420.819557 415.267451 413.763207 407.165085
## 15 522.781161 519.051447 500.171434 439.233986 434.044077 431.807865 426.050069
## 16 562.541464 559.068793 540.207230 479.274563 474.037852 471.843878 466.027362
## 17 588.815112 585.330575 566.429054 505.419741 500.078597 498.042521 492.066428
## 18 604.534325 601.091416 582.252673 521.322990 516.056147 513.892365 508.042397
## 19 627.025183 623.564471 604.859126 544.146756 539.019743 536.551838 531.055718
## 20 651.018037 647.646206 628.933131 568.186953 563.026000 560.621309 555.042265
## 21 674.840163 671.520344 652.845315 592.160173 587.009374 584.545065 579.045464
## 22 682.961695 679.707635 660.989382 600.230883 595.017848 592.667618 587.034056
## 23 691.722271 688.544224 669.669927 608.737634 603.241951 601.273453 595.297225
## 24 696.842193 693.621586 674.731431 613.733121 608.229546 606.329731 600.254256
## 25 706.971586 703.790644 684.890365 623.907978 618.351282 616.486385 610.407704
## 26 723.285308 720.084674 701.307169 640.454325 635.095326 632.950216 627.121370
## 27 730.920976 727.747483 709.042364 648.289698 643.034256 640.720200 635.057974
## 28 742.601214 739.461276 720.623443 659.626420 654.210356 652.249817 646.165135
## 29 755.306216 752.273874 733.307386 672.091014 666.514220 664.891460 658.403232
## 30 766.189402 763.139500 744.199991 683.023963 677.468043 675.790807 669.371847
## 9 10 11 12 13 14 15
## 2
## 3
## 4
## 5
## 6
## 7
## 9
## 10 135.548901
## 11 269.129677 134.875462
## 12 275.083977 140.326487 12.006148
## 13 302.165289 167.974471 33.153039 29.558261
## 14 318.145004 183.920811 49.147104 44.660450 16.104912
## 15 337.069380 202.279703 68.832986 62.025314 37.050452 22.558808
## 16 377.029054 242.212167 108.323739 102.049733 75.708206 59.896079 40.124463
## 17 403.020705 268.357408 134.131018 128.186761 101.258234 85.254254 66.356537
## 18 419.020860 284.266727 150.162545 144.081371 117.312940 101.347342 82.124235
## 19 442.060703 307.156790 173.457783 167.033308 140.732891 124.806820 105.040004
## 20 466.038963 331.160753 197.290142 191.028028 164.476649 148.514221 129.027129
## 21 490.032055 355.128738 221.314798 215.036591 188.498149 172.525754 153.047444
## 22 498.008506 363.151828 229.177825 223.040837 196.301743 180.309406 161.060670
## 23 506.186520 371.641311 237.493921 231.761615 204.615919 188.551596 170.084692
## 24 511.137440 376.629123 242.325566 236.660938 209.382846 193.330830 174.915122
## 25 521.277751 386.842581 252.633185 247.021684 219.758477 203.693013 185.386845
## 26 538.034619 403.341076 269.161396 263.274177 236.227448 220.191822 201.363182
## 27 546.005559 411.191057 277.140697 271.108279 244.232570 228.218309 209.140455
## 28 557.101013 422.510685 288.089090 282.407047 255.083992 239.064685 220.508629
## 29 569.356042 435.003939 300.361237 295.001903 267.304157 251.310275 233.265400
## 30 580.314063 445.928995 311.318378 305.901295 278.265673 262.266032 244.123376
## 16 17 18 19 20 21 22
## 2
## 3
## 4
## 5
## 6
## 7
## 9
## 10
## 11
## 12
## 13
## 14
## 15
## 16
## 17 26.422386
## 18 42.066644 16.233299
## 19 65.145376 39.838581 23.779245
## 20 89.036636 63.313585 47.177219 24.107934
## 21 113.060614 87.292898 71.200632 48.048439 24.106431
## 22 121.026298 95.099218 79.064868 56.194420 32.183494 8.604493
## 23 130.136697 103.906749 88.465431 66.800299 43.913466 23.816223 17.259803
## 24 134.907570 108.622880 93.072928 71.394275 48.083885 26.850698 19.109560
## 25 145.442645 119.180705 103.769689 82.162503 58.996664 37.470927 29.674732
## 26 161.298126 135.149077 119.300607 96.789005 72.824425 49.176447 40.811030
## 27 169.084028 143.058687 127.089260 104.277047 80.237834 56.302487 48.124681
## 28 180.442274 154.230677 138.402954 116.155293 92.120918 68.696373 60.277267
## 29 193.272216 166.980529 151.340936 129.648877 105.786090 82.864823 74.338169
## 30 204.110130 177.829110 162.141181 140.272717 116.337838 93.155904 84.661820
## 23 24 25 26 27 28 29
## 2
## 3
## 4
## 5
## 6
## 7
## 9
## 10
## 11
## 12
## 13
## 14
## 15
## 16
## 17
## 18
## 19
## 20
## 21
## 22
## 23
## 24 7.112138
## 25 15.804964 12.029231
## 26 33.047411 27.693878 20.261394
## 27 41.915898 36.713186 29.481540 9.434728
## 28 52.536959 46.787986 38.473892 20.534023 15.064103
## 29 65.603654 59.725262 51.208977 35.353286 30.643872 15.843879
## 30 76.007467 70.243025 61.376501 44.900316 39.046261 24.816287 11.092358
Agora as médias totais e entre trechos do rio
mean(env_dist) # Esse é o valor médio da similaridade de jaccard entre todas as combinações possíveis
## [1] 302.936
mean(dist_subset(env_dist, c(1:8))) # vai pegar as primeiras 9 linhas da matriz e calcular a similaridade média. Isso equivale a similaridade de alto rio
## [1] 79.71855
mean(dist_subset(env_dist, c(9:18))) # Agora para o médio rio
## [1] 105.052
mean(dist_subset(env_dist, c(19:28))) # Agora para o baixo rio
## [1] 41.48669
Tem coisa interessante aqui… o que será?
clust_env_euc<-hclust(env_dist, method = "complete")
clust_graf_env_euc<-plot(clust_env_euc, hang=-1)
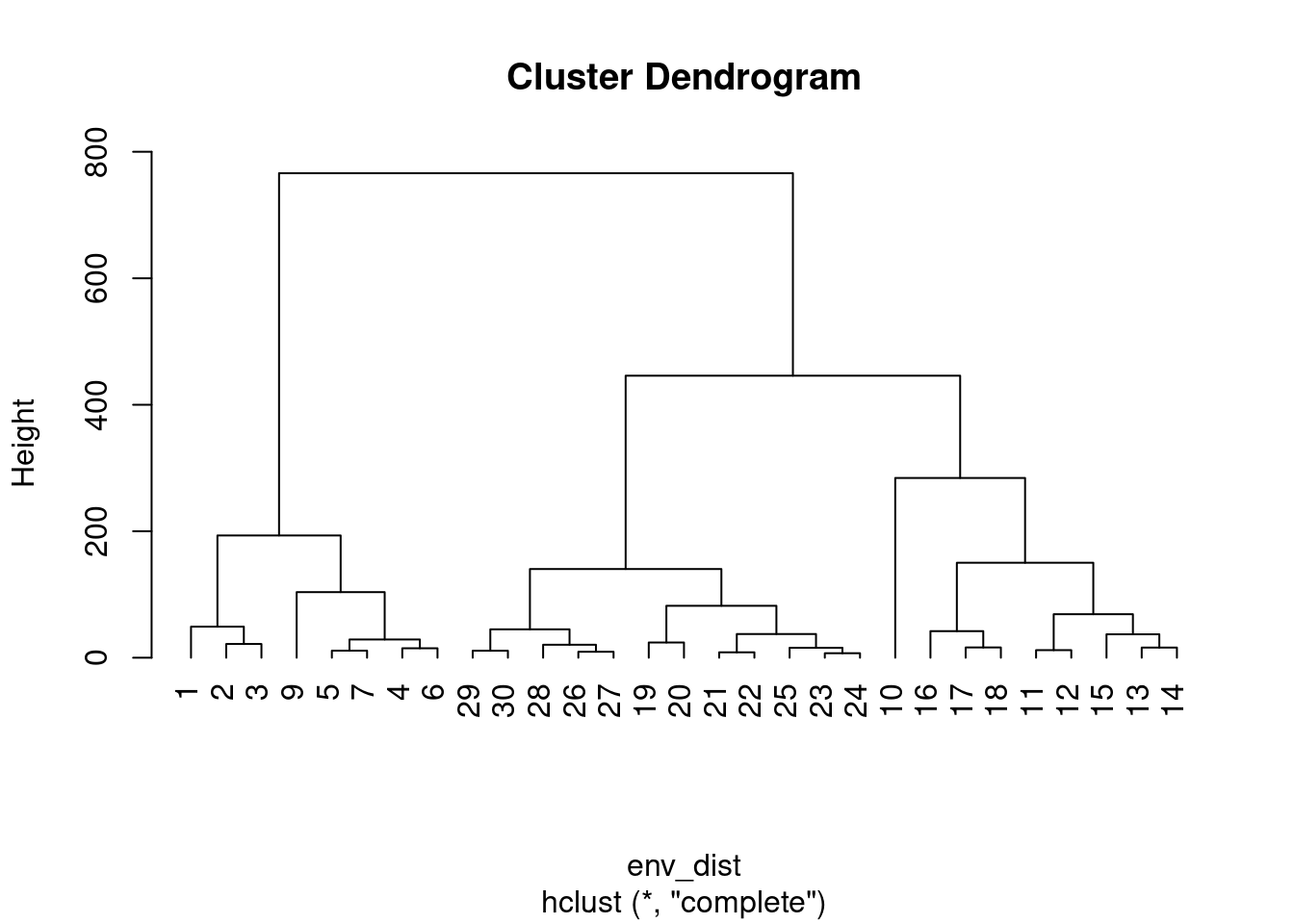
clust_graf_env_euc
## NULL
Vamos colorir o gráfico…
clust_graf_env_euc2<-as.dendrogram(clust_env_euc) # trandformando o cluster num objeto para poder editar
colors<-c("#E69F00","#56B4E9", "#009E73") # definindo as cores que serão usadas
colorCode<-c(alto=colors[1], medio=colors[2], baixo=colors[3])
labels_colors(clust_graf_env_euc2) <- colorCode[rio][order.dendrogram(clust_graf_env_euc2)]
Agora podemos plotar o dendograma onde: números amarelos são do alto rio, azuis do médio rio e pretos do baixo rio.
plot(clust_graf_env_euc2)
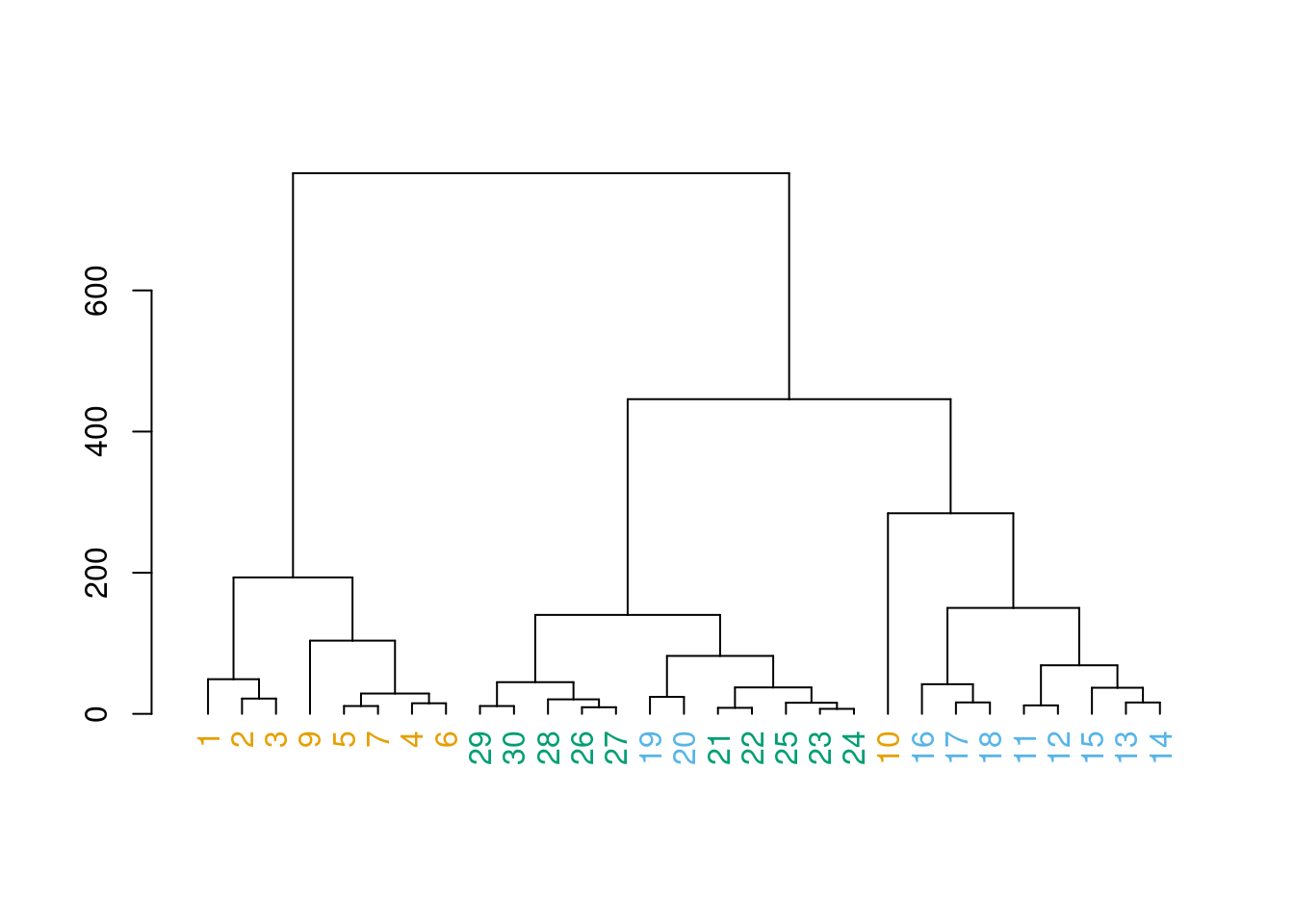
E agora? Dá pra entender?
Então, bora trabalhar!!!
